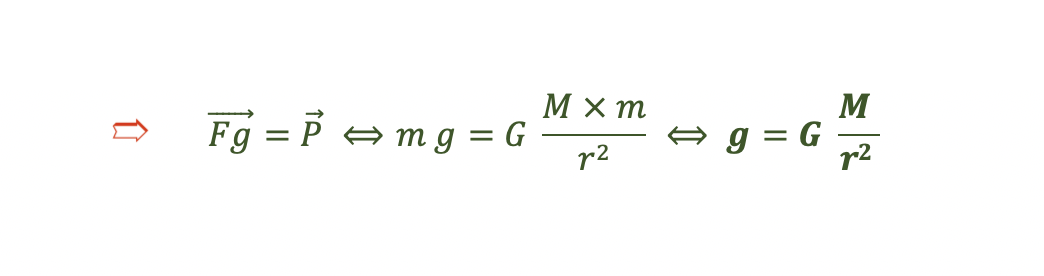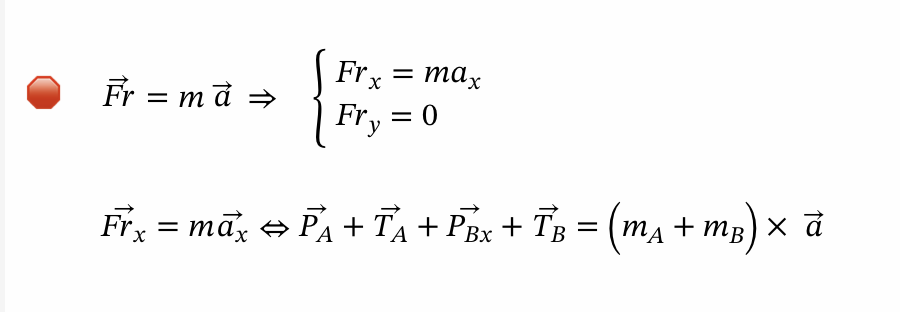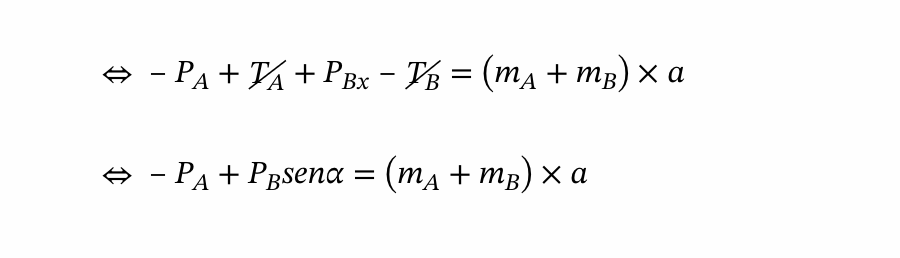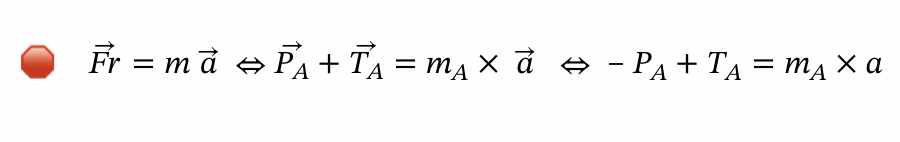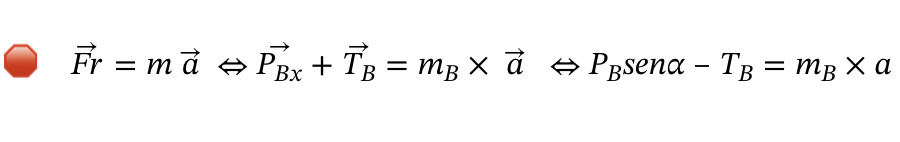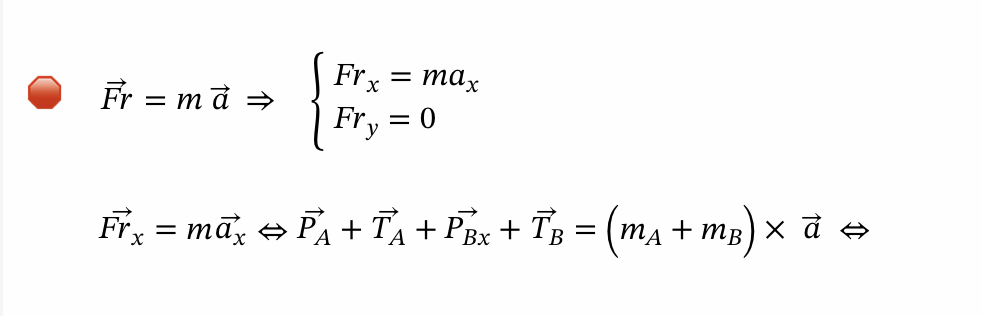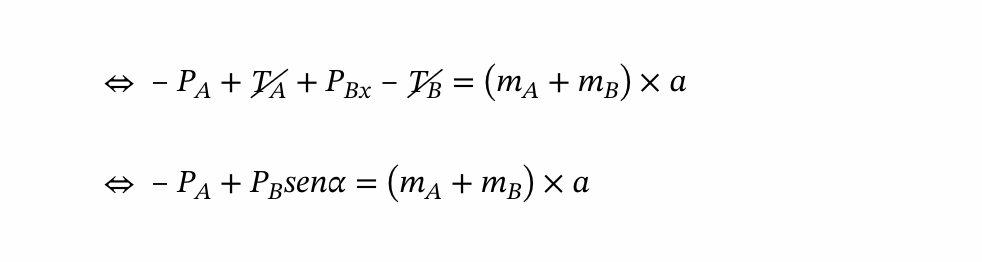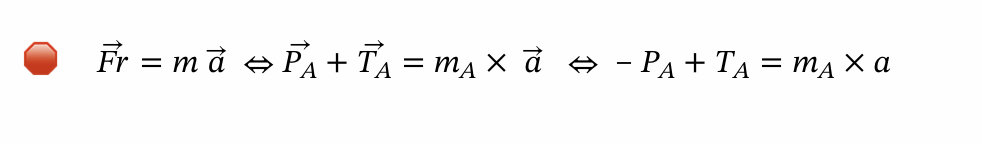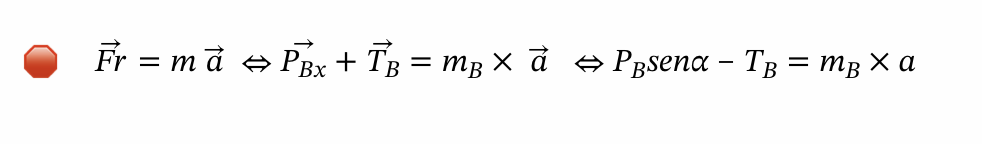- Aula nº5
⇒ Segunda Lei de Newton;
Um efeito da resultante das forças que atuam num corpo é a variação da sua velocidade, a qual está associada à aceleração.
Por isso, a resultante das forças terá de se relacionar com a aceleração.
Foi Newton quem primeiro relacionou a força e a aceleração por ela produzida, formulando uma Lei, conhecida por Segunda Lei de Newton ou Lei Fundamental da Dinâmica.
A resultante das forças, Fr, exercidas num sistema de massa constante, m, e a aceleração, a, do sistema relacionam-se por:
Fr = ma
Esta Lei permite tirar conclusões importantes:
🛑 Quanto maior for o módulo da resultante das forças aplicadas a um corpo, maior será o módulo da sua aceleração;
🛑 Um corpo terá movimento uniformemente variado se a resultante das forças que atuarem sobre ele for constante e tiver a mesma direção da velocidade inicial, sendo a aceleração constante;
🛑 A mesma resultante de forças aplicada a corpos de massas diferentes provocará menor aceleração, no corpo que tiver maior massa.
Os módulos da resultante das forças, Fr, e da aceleração, a, são diretamente proporcionais , sendo m a constante de proporcionalidade: o gráfico «resultante das forças – aceleração» é uma reta que passa pela origem, com declive positivo e igual -a massa do corpo (maior massa significa maior declive).
A mesma resultante de forças aplicada a corpos de massas diferentes
O corpo de massa maior resiste mais à variação de velocidade, pelo que adquire menor aceleração.
Esta propriedade chama-se inércia e é medida pela massa do corpo: quanto maior for a massa de um corpo, maior será a sua inércia, ou seja, maior a resistência à mudança de velocidade.
A massa é também designada por massa inercial.
Aceleração gravítica em função da distância
Como a resultante das forças é igual ao peso e a aceleração é a aceleração gravítica:
🛑 Fr = m a
🛑 P = m g
O módulo do peso é diretamente proporcional à massa, sendo g a constante de proporcionalidade, que é aproximadamente constante à superfície da Terra.
Quanto maior for a massa de um corpo, maior será o seu peso.
Igualando a lei da gravitação universal à resultante das forças é possível calcular o valor de g.
O módulo da aceleração gravítica, g, num dado ponto, só depende da distância desse ponto ao centro de massa da Terra, pois G e M são constantes: é inversamente proporcional ao quadrado da distância ao centro de massa da Terra.
Aplicação da Segunda Lei de Newton ao movimento retilíneo de corpos nos quais apenas atuam forças constantes.
🟡 Força horizontal a puxar um bloco num plano horizontal
Método de resolução:
Define-se um referencial xOy, fazendo coincidir um eixo com a direção do movimento; como no movimento retilíneo a aceleração tem a direção do movimento, só há aceleração nessa direção (na direção normal a aceleração é nula);
Aplicação da Segunda Lei de Newton ao movimento retilíneo de corpos nos quais apenas atuam forças constantes .
🟡 Força oblíqua a puxar um bloco num plano horizontal
Método de resolução:
Se as forças não tiverem a direção dos eixos, decompõem-se segundo essas direções, e determinam-se as suas componentes escalares;
🛑 Aplica-se a Segunda Lei de Newton usando equações escalares
- Forças aplicadas no centro de massa
- Decomposição da força F nas direções dos eixos dos xx e dos yy
Método de resolução:
Galileu procurou estudar movimentos verticais de corpos, verificou que esferas largadas a partir do repouso apresentam uma distância percorrida diretamente proporcional ao quadrado do tempo de descida.
Galileu concluiu que o tempo de descida não depende do peso ou do tamanho das esferas e é tanto menor quanto maior a inclinação da rampa.
Aplica-se a Segunda Lei de Newton usando equações escalares:
Método de resolução:
Aplica-se a Segunda Lei de Newton usando equações escalares
⇒ Para calcular o valor da aceleração:
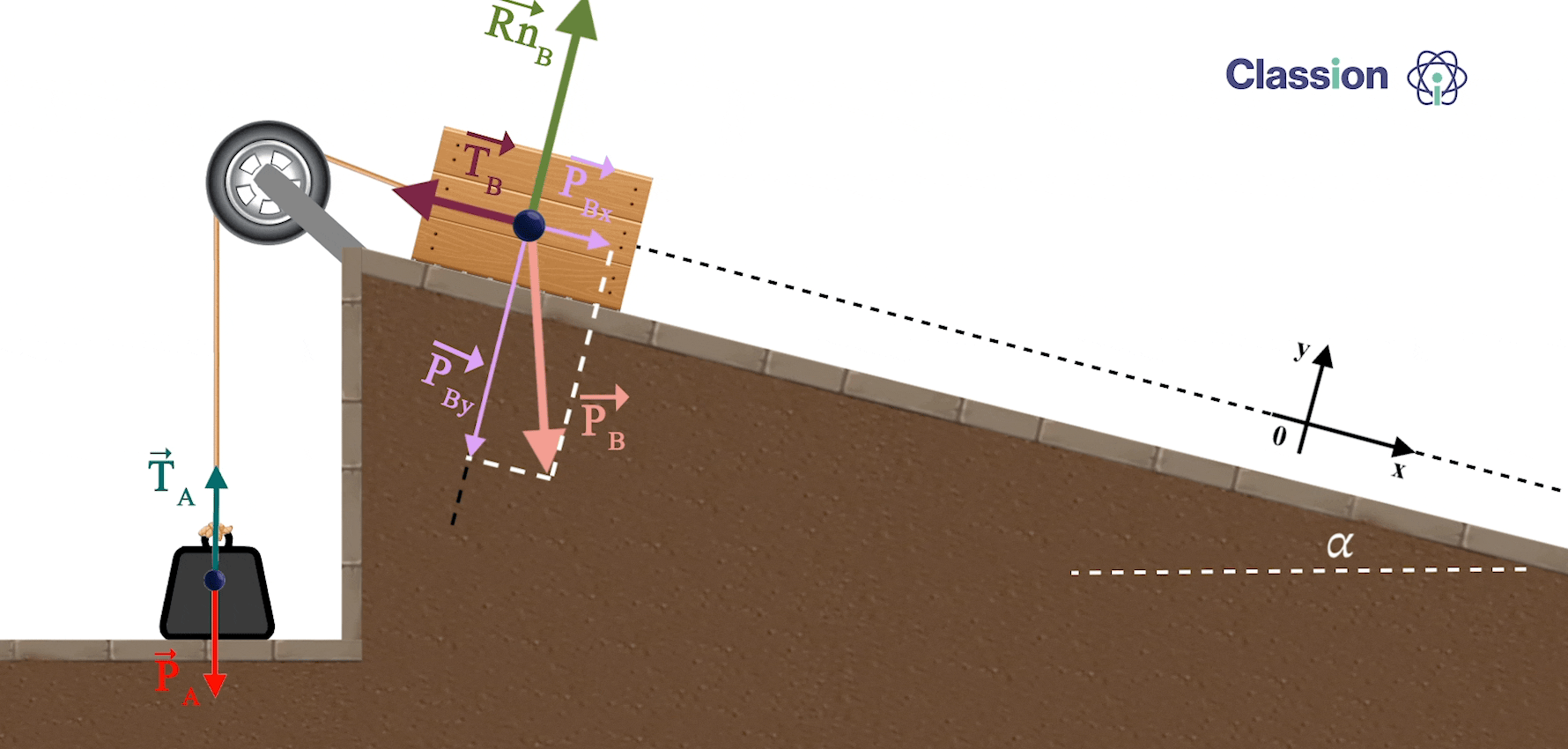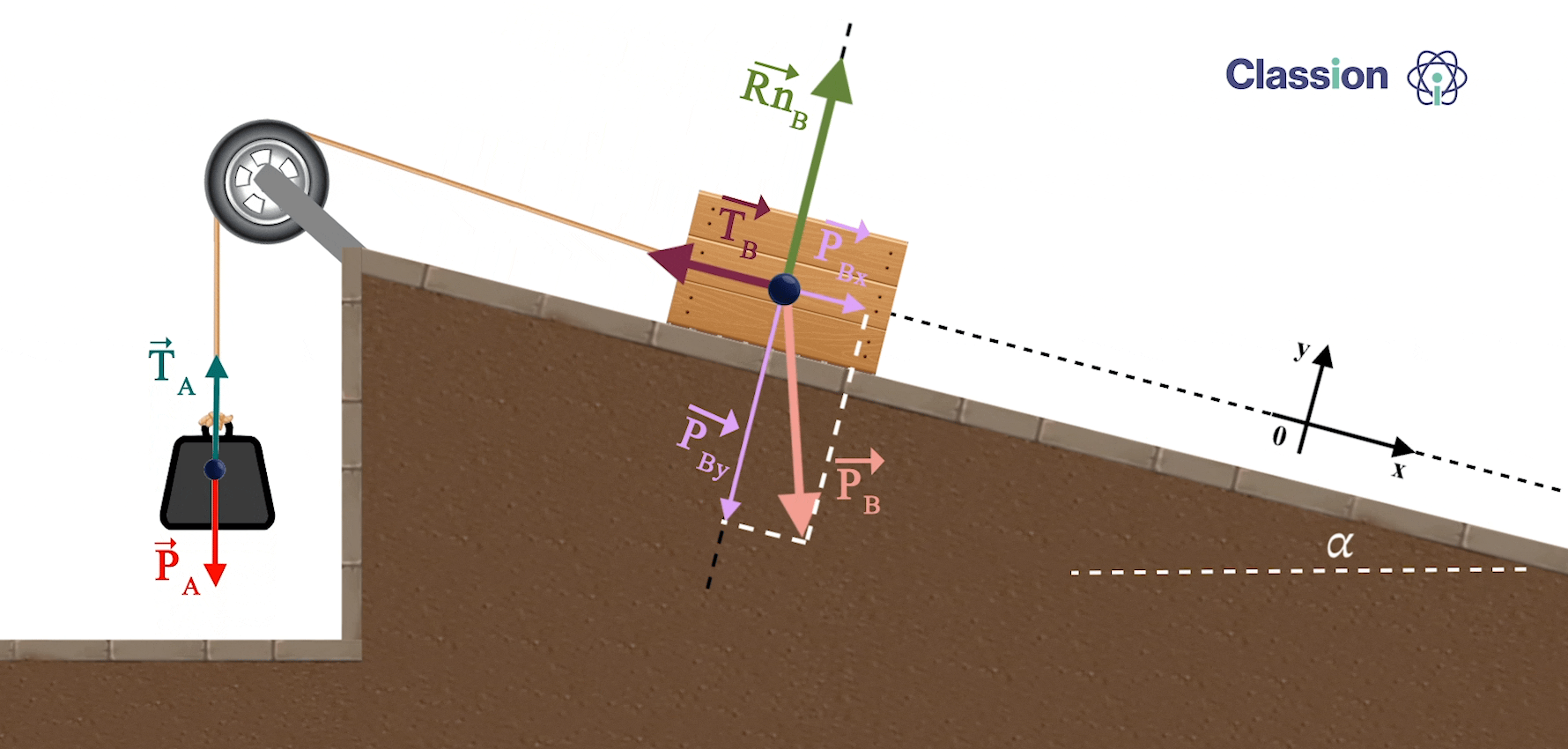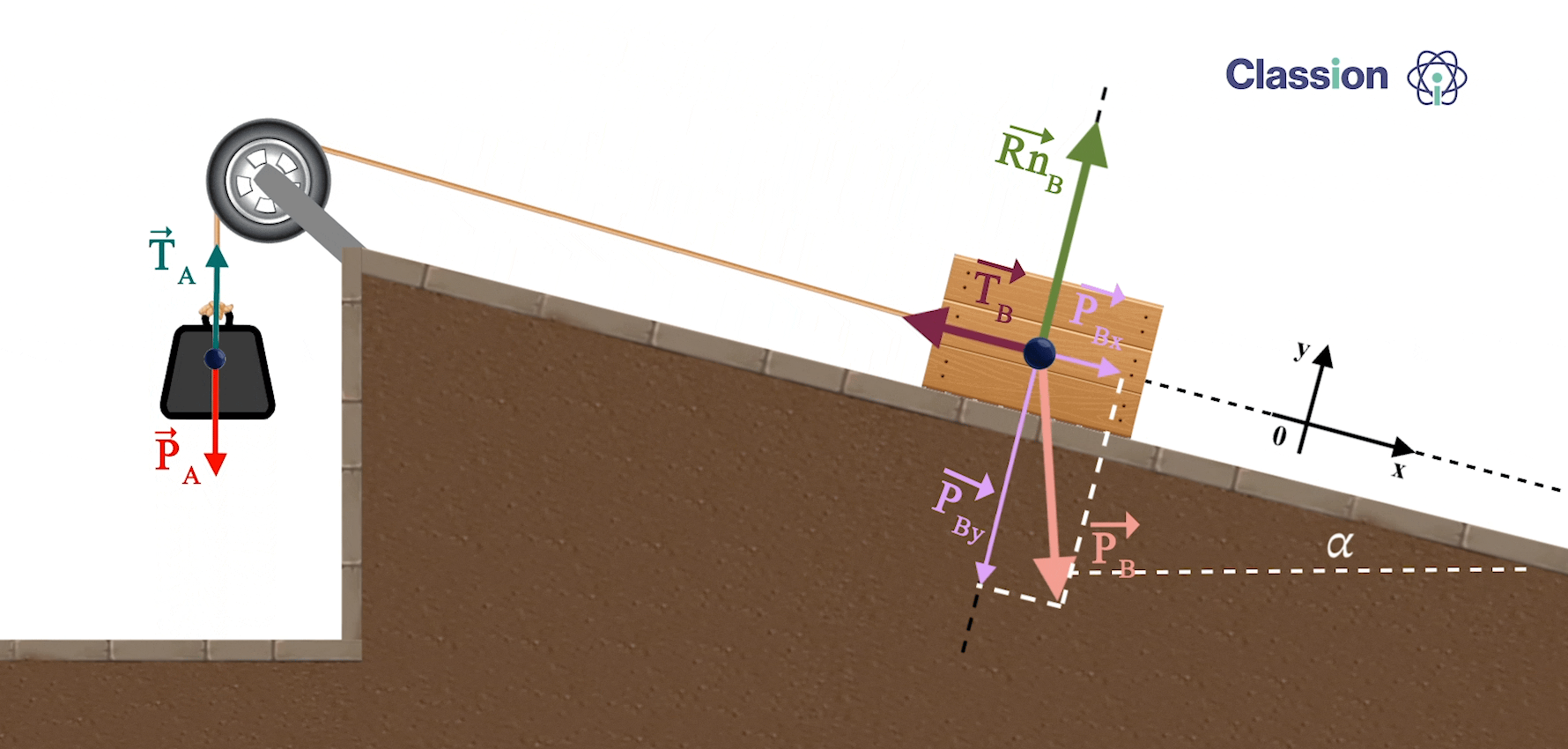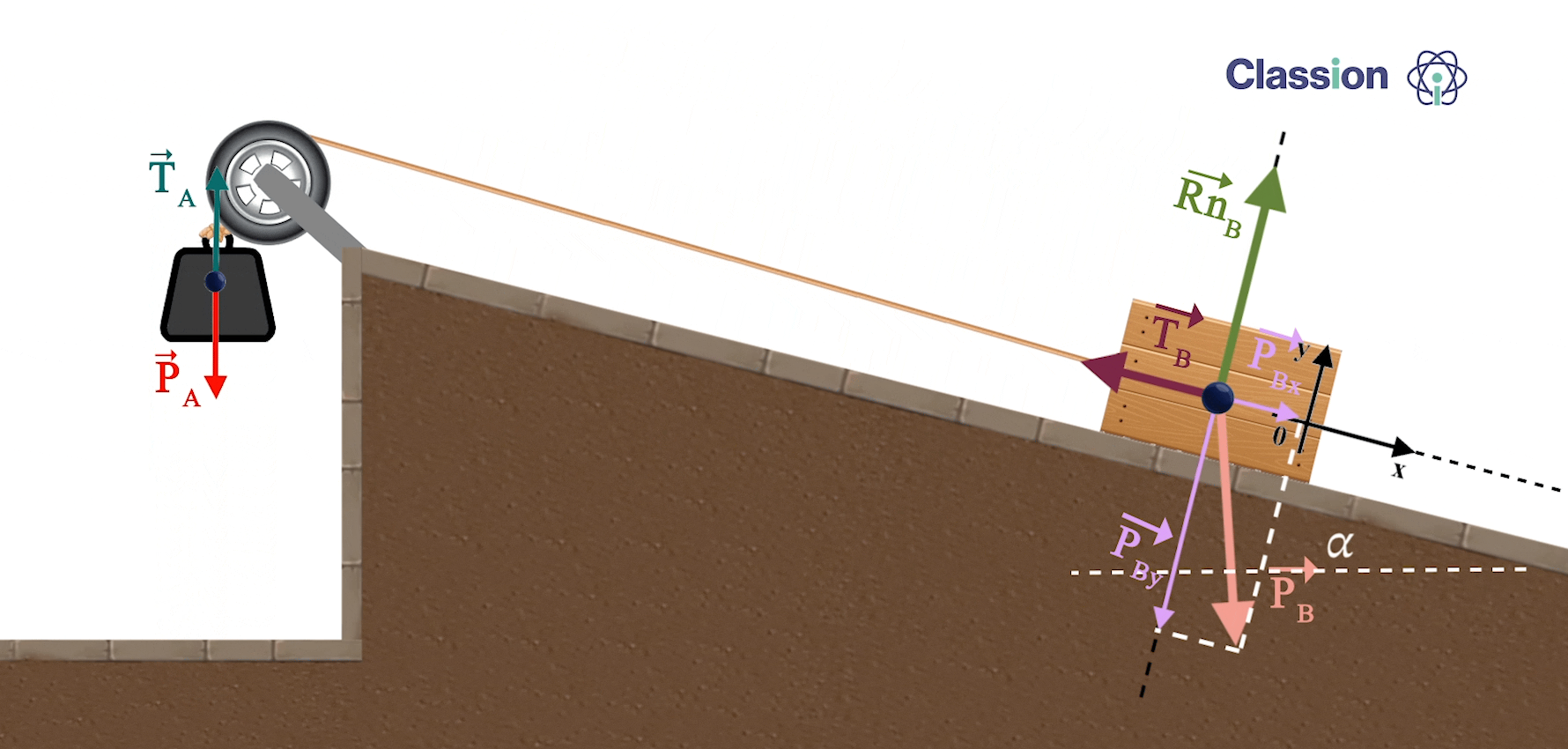
como a TA e TB tem igual intensidade mas de sentidos opostos, vamos considerar que o movimento é efetuado no sentido do corpo A para o corpo B.
Caso a aceleração seja negativa, significa que o sentido é o contrário ao considerado.
⇒ Para calcular o valor da tensão do fio:
- No corpo A:
- No corpo B:
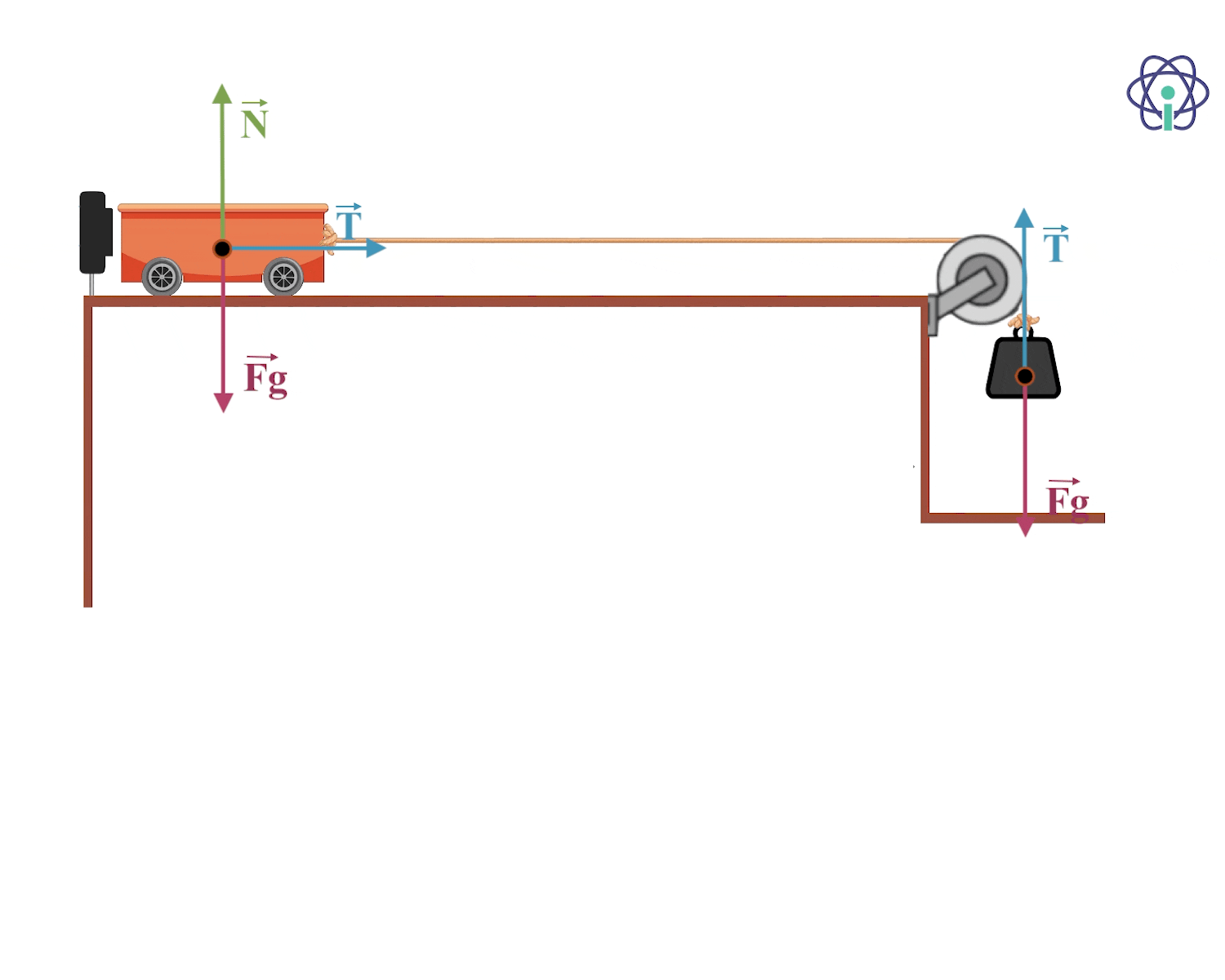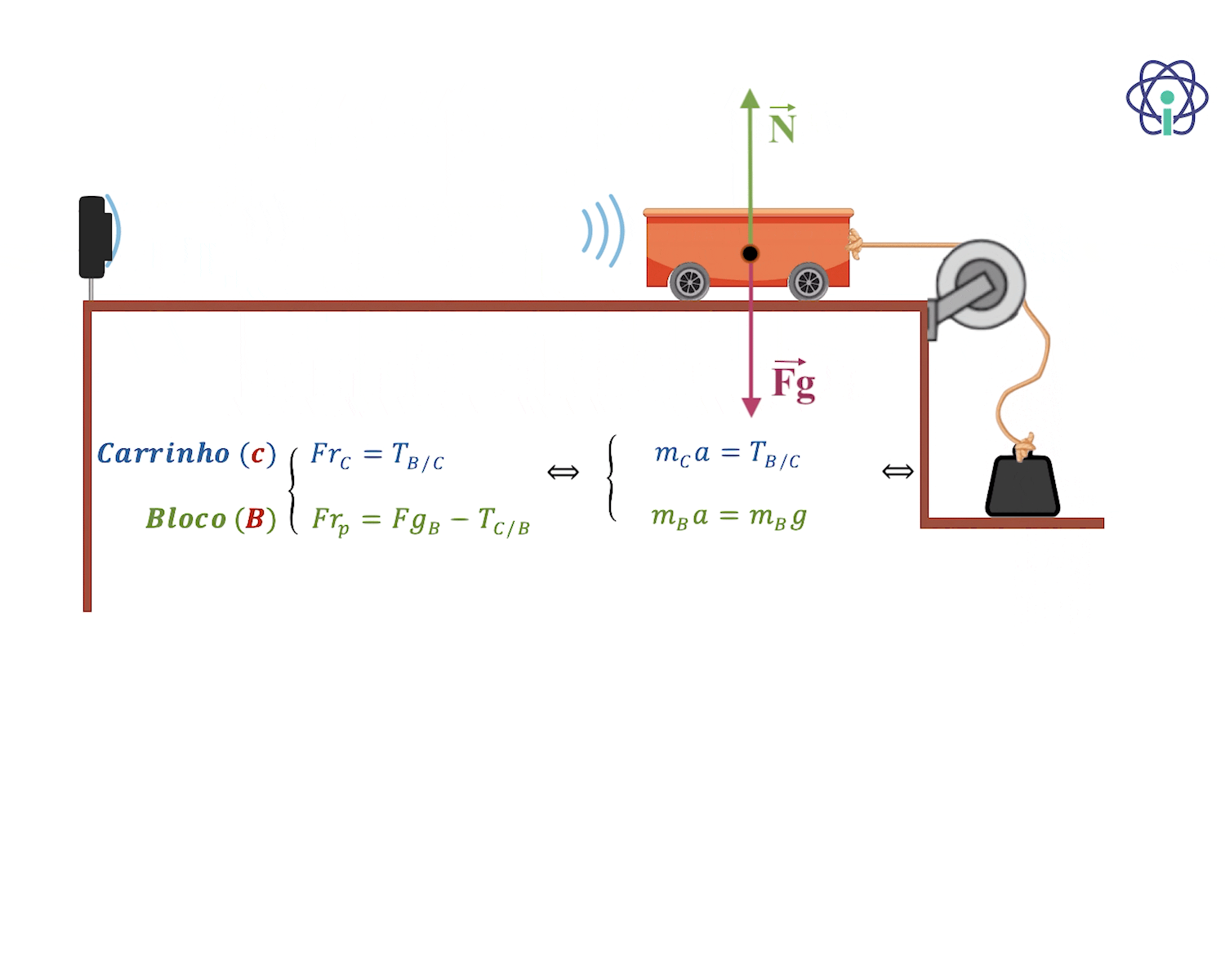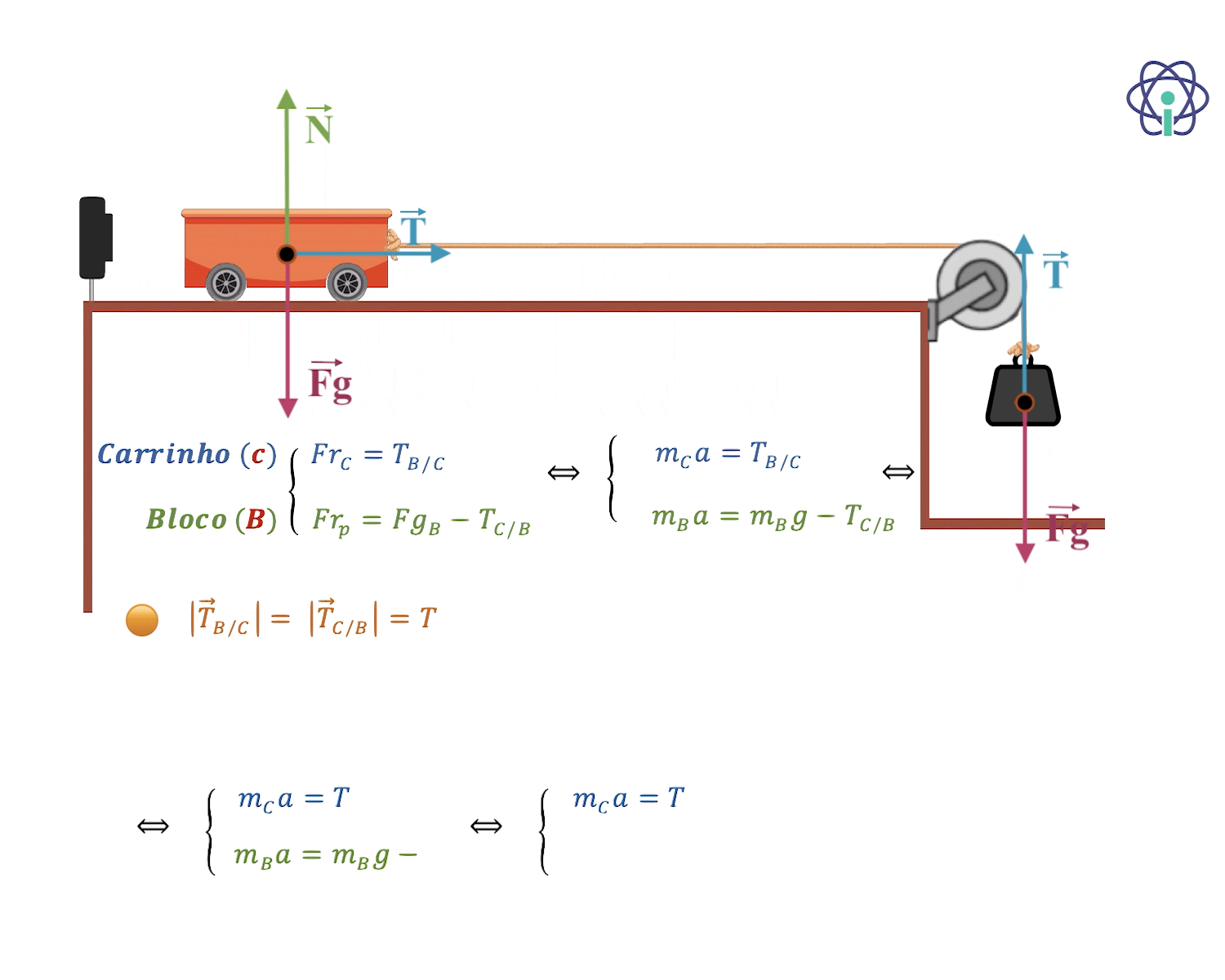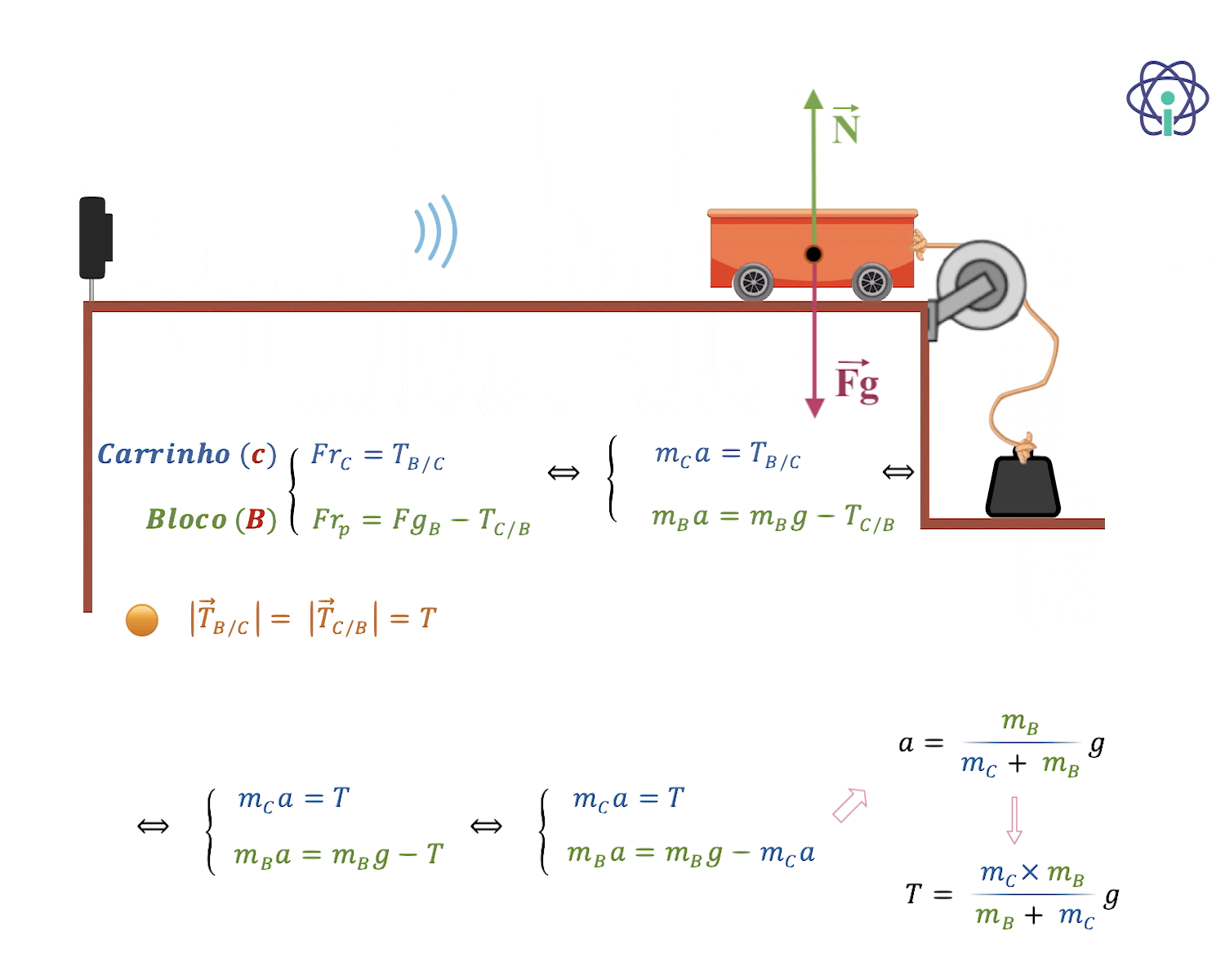
Método de resolução:
- Considera um corpo em movimento retilíneo numa superfície horizontal.
Aplica-se a Segunda Lei de Newton usando equações escalares
⇒ Para calcular o valor da aceleração:
como a TA e TB tem igual intensidade mas de sentidos opostos, vamos considerar que o movimento é efetuado no sentido do corpo A para o corpo B.
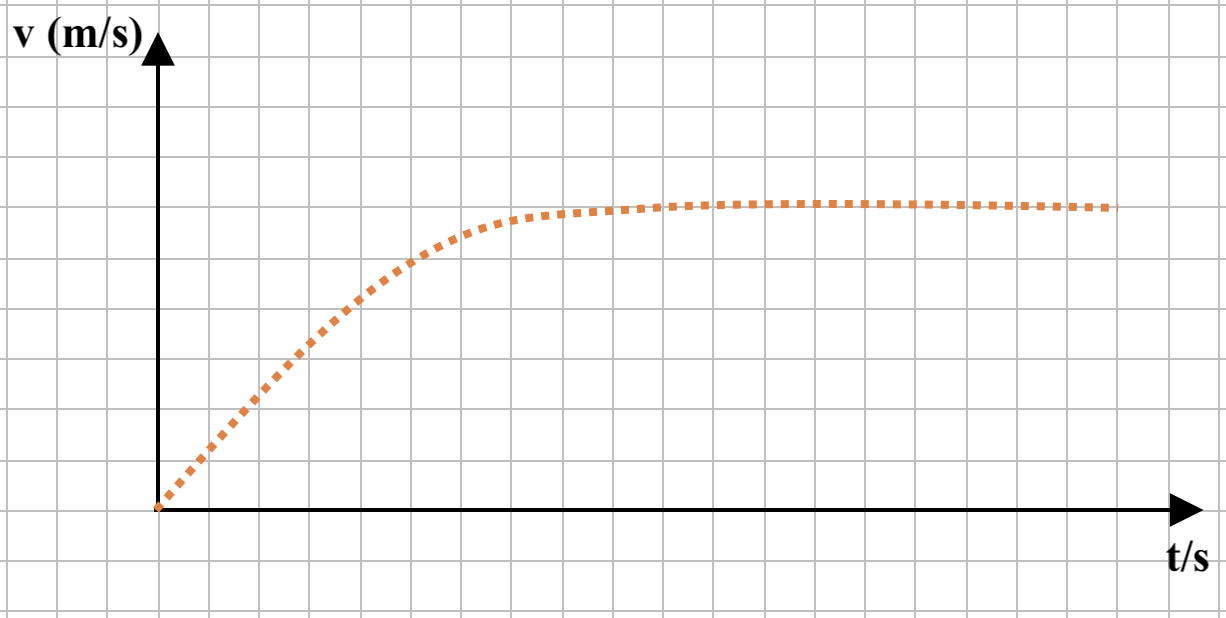
Antes de o corpo colidir com o solo, o tipo do movimento do carrinho é uniformemente acelerado (a velocidade do carrinho aumenta linearmente com o tempo).
⇒ Para calcular o valor da tensão do fio:
- No corpo A:
- No corpo B:
Tem uma resultante de forças nula (corpo B está no chão)
Depois de o corpo suspenso embater no solo, a força resultante a atuam no carrinho é nula e a velocidade deverá manter-se constante. O movimento do carrinho a partir desse instante deverá ser retilíneo uniforme.
♦ O gráfico que pode representar o módulo da velocidade do carrinho em função do tempo, nas duas partes do percurso, quer quando o fio o está a puxar, quer quando o fio deixa de estar em tensão.