Voltar a: 10ºAno – Física
Ficha nº1
Exercícios de exames e testes intermédios (2006 – 2022*)
10ºano – Física – Subdomínio 2 (Energia e fenómenos elétricos)
1. (2012 – 1ªF) Com o objetivo de determinar a capacidade térmica mássica do cobre e do alumínio, um grupo de alunos utilizou sucessivamente blocos calorimétricos desses metais, numa montagem semelhante à representada na Figura 2.
Os alunos começaram por introduzir um sensor de temperatura, ligado a um sistema de aquisição de dados, num dos orifícios de um desses blocos calorimétricos e uma resistência de aquecimento no outro orifício.
Tiveram, ainda, o cuidado de proceder de modo a otimizar o contacto térmico do bloco, quer com o sensor, quer com a resistência, e a minimizar a taxa de dissipação de energia do bloco.
Seguidamente, os alunos montaram um circuito elétrico, ligando a resistência de aquecimento a uma fonte de alimentação, a um voltímetro, a um amperímetro e a um interruptor.
1.1. Qual dos esquemas seguintes pode representar o circuito elétrico montado pelos alunos?
- Opção (B)
⇒ O esquema que pode representar o circuito montado é o representado em (B), uma vez que (para medir a intensidade da corrente que percorre o circuito) o amperímetro terá de ser ligado em série enquanto (para medir a diferença de potencial entre os terminais da resistência de aquecimento) o voltímetro terá de ser ligado em paralelo.
- Opção (B)…………. 5 pontos
1.2. Os alunos ligaram o interruptor do circuito elétrico e iniciaram, simultaneamente, o registo da temperatura do bloco de cobre em função do tempo.
Identifique uma das grandezas que os alunos tiveram de medir para calcularem a potência dissipada pela resistência de aquecimento.
⇒ A diferença de potencial ou a intensidade da corrente elétrica.
⇒ Para calcularem a potência dissipada pela resistência de aquecimento, os alunos tiveram de recorrer à lei de Joule, P = I U, pelo que tiveram de medir a diferença de potencial, U, entre os terminais da resistência e a intensidade da corrente elétrica, I, que percorre o circuito.
- Diferença de potencial ou Tensão ou Intensidade de corrente …………. 8 pontos
2. (2017 – EE) A Figura 1 representa parte de uma montagem utilizada na determinação experimental da capacidade térmica mássica do cobre. Nessa montagem, o sensor de temperatura estava ligado a um sistema de aquisição de dados, e a resistência de aquecimento estava inserida num circuito elétrico.
Com o objetivo de determinar indiretamente a potência fornecida pela resistência de aquecimento ao bloco de cobre, introduziram-se, no circuito elétrico, dois aparelhos de medida (multímetros).
Indique o nome das duas grandezas elétricas que, na experiência realizada, foram medidas com os multímetros.
⇒ Um multímetro é um aparelho que pode ser utilizado como voltímetro – mede a diferença de potencial (U) entre os terminais do condutor –, como amperímetro – mede a corrente elétrica (I) que percorre o condutor –, ou como ohmímetro – mede a resistência (R) do condutor.
⇒ Pela Lei de Joule, vem:
- (1) P = R I2
⇒ Mas da Lei de Ohm têm-se:
- (2) R = U/I ⇒ P = UI
ou
- (3) I = U/R ⇒ P = U2/R
⇒ Assim, e consoante a expressão a utilizar, os alunos deveriam medir:
– A resistência elétrica e a corrente elétrica (1).
– A diferença de potencial e a corrente elétrica (2)
– A diferença de potencial e a resistência elétrica (3).
- Diferença de potencial [elétrico] e corrente elétrica. …………. 5 pontos
ou
- Diferença de potencial [elétrico] e resistência [elétrica].
ou
- Corrente elétrica e resistência [elétrica].
Nota – A referência a «Intensidade da corrente elétrica» não implica qualquer desvalorização.
3. (2019 – 1ªF) Num ensaio laboratorial, adicionou-se uma amostra de água, a uma temperatura T, a uma outra amostra de água, de massa 350,0 g e inicialmente a 5,2 ºC.
Verificou-se que, após um determinado intervalo de tempo, o sistema resultante daquela adição ficou à temperatura de 27,9 ºC.
As temperaturas foram medidas com um termómetro digital, cujo funcionamento se baseia na variação da resistência elétrica de um fio condutor (constituinte do termómetro) com a temperatura.
Para que o termómetro funcione adequadamente, a variação da potência dissipada por efeito Joule, no fio, deve ser desprezável.
Considere que a resistência elétrica do fio aumenta 3,85 Ω por cada 10 ºC de aumento de temperatura e que, na experiência realizada, o fio foi percorrido por uma corrente constante de 9,0 x 10-4 A.
Verifique que, entre 5,2 ºC e 27,9 ºC, o aumento da potência dissipada naquele fio foi inferior a 10-5 W, sendo, por isso, desprezável.
Apresente todas as etapas de resolução, explicitando todos os cálculos efetuados.
⇒ Como existiu uma variação de temperatura de 22,7 ºC, pode-se considerar que a resistência elétrica aumentou de forma proporcional à variação de temperatura:
⇒ A potência dissipada pode ser calculada pela Lei de Joule, Pdiss = R I2, o que significa que uma variação de resistência, ΔR, corresponde a uma variação de potência dissipada,
ΔPdiss = ΔR I2 , ou seja, ΔPdiss = 8,74 x (9,0 x 10−4)2 W = 7,1 x 10-6 W
- Como o valor calculado é inferior a 10-5 W, pode ser considerado desprezável.
- Etapas de resolução:
⇒ Cálculo do aumento da resistência do fio (ΔR = 8,74 Ω) …….. 5 pontos
⇒ Cálculo do aumento da potência dissipada no fio (ΔP = 7,1 x 106 W ) …….. 4 pontos
⇒ Comparação do aumento da potência dissipada no fio com 10-5 W (ΔP < 10-5 W) …….. 1 pontos
4. (2019 – 2ªF) Numa aula laboratorial, os alunos colocaram num calorímetro 90 g de água, na qual mergulharam um fio condutor eletricamente isolado, de resistência elétrica R.
Para aquecer a água, fizeram passar nesse fio, durante 180 s, uma corrente elétrica I, tendo determinado o aumento da temperatura, ΔT, da água, nesse intervalo de tempo. Repetiram a experiência para diferentes valores de corrente elétrica.
Um aluno traçou, a partir dos resultados experimentais obtidos, um gráfico cujo esboço se encontra representado na Figura 2.
Nesse esboço, X pode representar
(A) R
(B) R2
(C) I
(D) I2
- Opção (D)
⇒ Numa resistência elétrica, 𝑅, percorrida por uma corrente elétrica, 𝐼, é dissipada uma potência, 𝑃, por efeito Joule:
𝑃 =𝑅𝐼2
⇒ Num intervalo de tempo Δt é dissipada pela resistência elétrica a energia 𝐸 (𝐸 = 𝑃Δt = 𝑅 𝐼2 Δt).
⇒ Esta energia será recebida pela massa, 𝑚, de água, de capacidade térmica mássica 𝑐, originando o seu aquecimento, com o consequente aumento de temperatura, Δ𝑇.
Relacionando aquelas grandezas obtém-se 𝑚 𝑐 Δ𝑇 = 𝑅 𝐼2 Δt , ou, explicitando em ordem à variação de temperatura:
Na experiência, fixaram-se a massa de água, a resistência elétrica e o intervalo de tempo, assumindo-se que a capacidade térmica mássica da água é constante.
⇒ Assim, as grandezas variáveis são a corrente elétrica e a variação de temperatura, tal como referido no enunciado “determinando o aumento de temperatura” e “diferentes valores de corrente elétrica”.
- Como o gráfico obtido apresenta uma relação linear, o aluno colocou o quadrado da corrente elétrica no eixo das abcissas.
𝑋 = 𝐼2 ⟹ Δ𝑇 = 𝑘 𝑋
- Opção (D) ……………. 7 pontos
5. (2020 – 1ªF) Na Figura 5, está representado um circuito elétrico com:
• um gerador de força eletromotriz 9,20 V e resistência interna 2,0 Ω ;
• um voltímetro ligado nos terminais do gerador;
• dois condutores, A e B, de resistências elétricas RA e RB , sendo RA = 3 RB.
Determine a potência dissipada no condutor A quando o voltímetro marca 8,74 V.
Explicite o seu raciocínio, indicando todos os cálculos efetuados.
A pontuação obtida na resposta contribui obrigatoriamente para a classificação final da prova.
⇒ A corrente elétrica, I, fornecida pelo gerador, obtém-se a partir da expressão U = ε – rI, que relaciona a diferença de potencial elétrico, U, nos terminais do gerador, com a sua força eletromotriz ε e a sua residência interna, r.
⇒ Usando os dados, temos:
- 8,74 V = 9,20 V – 2,0 Ω x I ⇒ I = 0,230 A
⇒ As diferenças de potencial elétrico nos terminais dos condutores são iguais:
- UA = UB
⇒ A resistência do condutor A é triplo da do condutor B:
- RA = 3 RB
⇒ Por outro lado, verifica-se que I = IA + IB, onde IA e IB designam as correntes elétricas nos condutores A e B, respetivamente.
⇒ Usando as relações anteriores, temos:
⇒ A resistência do condutor A, RA, calcula-se a partir de:
- UA = RA x IA ⇒ 8,74 = RA x 0,0575 ⇒ RA = 152 Ω
⇒ A potência dissipada no condutor A é:
- Pdiss,A = RA IA2 = 152 x (0,0575)2 = 0,50 W
ou
⇒ Como a potência dissipada no condutor é igual à potência elétrica que recebe do gerador, pode obter-se o mesmo resultado, a partir de:
- Pdiss,A = UA IA = 8,74 x 0,0575 = 0,50 W
- Determina o valor solicitado, percorrendo as etapas seguintes:
⇒ Calcula a corrente elétrica fornecida pelo gerador (I = 0,230 A) …….. 3 pontos
⇒ Calcula a corrente elétrica que percorre o condutor A ( IA = 5,75 x 10-2 A)
ou
- Obtém uma expressão que relaciona a potência dissipada no condutor A com a potência fornecida pelo gerador ( 4 PA = PG) …….. 4 pontos
⇒ Calcula a potência dissipada no condutor A (PA = 0,50 W) …….. 3 pontos
6. (2020 – 2ªF) O circuito elétrico representado na Figura 2 é constituído por um gerador ideal (um gerador cuja resistência interna pode ser considerada nula), um reóstato T e um interruptor.
Conclua como varia a potência dissipada no reóstato T quando a resistência elétrica introduzida por esse reóstato aumenta.
Mostre como chegou à conclusão solicitada.
A pontuação obtida na resposta contribui obrigatoriamente para a classificação final da prova.
⇒ Dado que o gerador é ideal (ri = 0), a diferença de potencial, U, nos seus terminais é constante, independente da corrente elétrica, I, e igual à sua força eletromotriz.
⇒ Considerando desprezável a energia dissipada nos fios de ligação e no interruptor, a diferença de potencial entre os terminais do reóstato é igual à diferença de potencial entre os terminais do gerador, logo constante.
⇒ O valor da diferença de potencial entre os terminais do reóstato é, para cada valor de resistência, R
- U = RI
Assim, quando a resistência aumenta, a corrente elétrica diminui, e como a potência dissipada neste dispositivo é
- P = UI
⇒ conclui-se que o valor desta diminui com o aumento da sua resistência.
ou
⇒ Sendo desprezável a resistência interna, r, do gerador, a diferença de potencial elétrico nos seus terminais é igual à sua força eletromotriz,
- ε (Ug = ε – I r ; r = 0 ⇒ Ug = ε)
constante, dado que o gerador é ideal.
⇒ Como apenas um reóstato está ligado ao gerador, pode considerar-se que estes componentes têm terminais comuns (os fios condutores que ligam o gerador ao reóstato têm resistências elétricas desprezáveis) e a diferença de potencial elétrico nos terminais do gerador, Ug, é a mesma que nos terminais do reóstato.
- UR (Ug = UR)
Assim, a diferença de potencial nos terminais do reóstato, UR, igual a ε, é também constante.
⇒ Com o aumento da resistência, R, do reóstato a corrente elétrica diminui (I = UR/R), logo, a potência dissipada, Pdiss = UR I, no reóstato, diminui.
7. (2020 – EE) Considere o circuito esquematizado na Figura 5, em que R1 e R2 representam dois condutores óhmicos e G é um gerador que pode ser considerado ideal (um gerador cuja resistência interna pode ser considerada nula).
Quando o interruptor k2 está aberto, é medida uma corrente elétrica I no amperímetro (ideal).
Preveja se a corrente elétrica medida pelo amperímetro aumenta, diminui ou se mantém constante quando se fecha o interruptor k2.
Mostre como chegou à previsão solicitada.
A pontuação obtida na resposta contribui obrigatoriamente para a classificação final da prova.
⇒ Sendo o gerador ideal, a f.e.m. é igual à diferença de potencial, pois, como U = ε – rI, em que r seria a resistência interna do gerador, que é nula num gerador ideal .
- U = ε
⇒ Como os dois condutores óhmicos R1 e R2 estão ligados em paralelo, a diferença de potencial elétrico nos terminais do gerador é igual à diferença de potencial elétrico nos terminais do condutor R1, quer o interruptor esteja aberto ou fechado.
⇒ De acordo com a Lei de Ohm, U = RI, e como a diferença de potencial elétrico nos terminais do gerador, U, é igual à diferença de potencial elétrico nos terminais do condutor R1, quer o interruptor K2 esteja aberto ou fechado, conclui-se que a diferença de potencial elétrico nos terminais do gerador é independente da corrente.
- A corrente elétrica medida pelo amperímetro mantém-se constante quando se fecha o interruptor K2 .
ou
Quando o interruptor está aberto e no amperímetro passa uma corrente I1, vem que U = R1 I1.
⇒ Quando o interruptor está fechado, admita-se que no amperímetro passa uma corrente I2.
⇒ Neste caso, a diferença de potencial seria U = R1 I1 , mas sendo U = ε, que se mantém constante, então R1 I1 = R2 I2
- I1 = I2, o que evidencia que a corrente elétrica medida pelo amperímetro se mantém constante quando se fecha o interruptor K2.
8. (2021 – 1ªF) Um LED (Light Emitting Diode) é um dispositivo que emite luz com elevada eficiência.
Na Figura 2, representa-se o gráfico da corrente elétrica, I, num LED, em função da diferença de potencial elétrico, U, nos seus terminais (curva característica do LED).
Para se obter a curva característica do LED, montou-se um circuito no qual o LED se encontrava ligado em série a um reóstato e a uma pilha ideal (pilha cuja resistência interna pode ser considerada nula) de forçaa eletromotriz 4,50 V.
Nesse circuito, introduziram-se ainda dois aparelhos de medida adequados.
8.1. Qual dos esquemas seguintes representa o circuito que permite obter a curva característica do LED?
A pontuação obtida na resposta contribui obrigatoriamente para a classificação final da prova.
- Opção (B)
⇒ O esquema de circuito elétrico que permite obter a curva característica do LED é
Notas:
⇒ Na Figura 2 do enunciado da prova, representa-se o gráfico da corrente elétrica, 𝐼, num LED, em função da diferença de potencial elétrico, 𝑈, nos seus terminais, pelo que o voltímetro tem de ser ligado aos terminais do LED.
- Opção (B) ……………. 10 pontos
8.2. Caso os terminais do LED tivessem sido ligados diretamente à pilha, a corrente elétrica seria superior à que o LED suporta e este acabaria por se queimar. Ao introduzir-se o reóstato em série no circuito, a corrente elétrica no LED pode ser controlada.
Determine qual deverá ser o valor da resistência elétrica mínima introduzida pelo reóstato, para que a corrente elétrica no LED não exceda 20 mA.
Apresente todos os cálculos efetuados.
A pontuação obtida na resposta contribui obrigatoriamente para a classificação final da prova.
⇒ Leitura a partir do gráfico da diferença de potencial elétrico nos terminais do LED quando a corrente elétrica que o atravessa é de 20,0 mA:
- O gráfico mostra que, quando a corrente elétrica no LED é de 20,0 mA, a diferença de potencial elétrico nos seus terminais é de 1,950 V (máximo da diferença de potencial elétrico em “condições de segurança”).
⇒ Cálculo do valor mínimo para a diferença de potencial elétrico nos terminais do reóstato, em condições de segurança:
- Considerando o esquema do circuito elétrico usado para obter a curva característica do LED, conclui-se que a diferença de potencial elétrico nos terminais da pilha, 𝑈, é igual à soma da diferença de potencial nos terminais do LED, 𝑈LED, com a diferença de potencial nos terminais do reóstato, 𝑈reóstato.
- Considerando que a pilha é ideal (a resistência interna da pilha, 𝑟, é considerada nula), a diferença de potencial elétrico nos terminais da pilha, 𝑈=𝜀−𝑟 𝐼, é igual à sua força eletromotriz, 𝜀.
Assim,
- 𝑈 = 𝑈LED + 𝑈reóstato ⟶ 4,50 V = 1,950 V + 𝑈reóstato ⇔ 𝑈reóstato = 2,55 V
⇒ Cálculo do valor mínimo da resistência elétrica introduzida pelo reóstato, 𝑅reóstato_mín, em condições de segurança:
- Usando a equação de definição de resistência elétrica, tem-se:
𝑅reóstato_min = 𝑈reóstato/𝐼máx = 2,55 V / 20×10−3 A ⇔ 𝑅reóstato_min = 1,3 × 102 Ω
Nota:
⇒ No limite das “condições de segurança”, a resistência elétrica do material semicondutor do LED é:
- 𝑅LED_mín = 𝑈LED_máx/𝐼máx = 1,950 V/ 20×10−3 A = 98 Ω
- Determina o valor solicitado, percorrendo as etapas seguintes:
⇒ Obtém, a partir do gráfico, a diferença de potencial nos terminais do LED para uma corrente elétrica de 20 mA (1,95 V) ………… 2 pontos
⇒ Calcula a diferença de potencial elétrico mínima nos terminais do reóstato (2,55 V) ……. 4 pontos
⇒ Calcula o valor da resistência elétrica mínima introduzida pelo reóstato (1,3 x 102 Ω) ……. 4 pontos
9. (2021 – 2ªF) As baterias e as pilhas são geradores de tensão contínua.
9.1. Considere duas baterias ideais (baterias cujas resistências internas podem ser consideradas nulas) idênticas e dois componentes puramente resistivos, P e Q , de resistências 8 kΩ e 24 kΩ , respetivamente.
Uma das baterias é ligada a P e a outra é ligada a Q.
A energia fornecida a P, relativamente à energia fornecida a Q , num mesmo intervalo de tempo, é
(A) 9 vezes menor.
(B) 3 vezes menor.
(C) 3 vezes maior.
(D) 9 vezes maior.
- Opção (C)
⇒ A energia fornecida a P, relativamente à energia fornecida a Q, num mesmo intervalo de tempo, é 3 vezes maior.
Notas:
⇒ Para uma bateria real:
- 𝑈 = 𝜀 − 𝑟 𝐼
⇒ Considerando que as duas baterias são ideais (baterias cujas resistências internas podem ser consideradas nulas) idênticas e cada uma delas está ligada só a um dos dois recetores, conclui-se que as diferenças de potencial elétrico nos terminais desses recetores são iguais:
- 𝑈P = 𝑈Q = 𝑈 = 𝜀
⇒ A energia elétrica fornecida a um recetor num dado intervalo de tempo está relacionada com a diferença de potencial elétrico nos terminais pela expressão:
- 𝐸el. = 𝑈 𝐼 Δ𝑡
⇒ Sendo os recetores puramente resistivos, essa energia também pode ser obtida a partir da expressão:
- 𝐸el = 𝑅 𝐼2 Δ𝑡
⇒ Usando a equação de definição de resistência elétrica e substituindo na última expressão, obtém-se:
- concluindo-se que para a mesma diferença de potencial elétrico e para o mesmo intervalo de tempo, a energia elétrica fornecida a um recetor é inversamente proporcional à sua resistência elétrica.
⇒ Assim:
- Opção (C) ……………. 10 pontos
9.2. Considere duas pilhas novas, X e Y, com as mesmas características.
A pilha X foi utilizada para alimentar um circuito elétrico durante um intervalo de tempo significativo.
A pilha Y não foi utilizada.
Qual dos esboços de gráfico seguintes pode traduzir as diferenças de potencial elétrico, U, nos terminais das pilhas X e Y, em função da corrente elétrica, I, fornecida?
- Opção (A)
⇒ O esboço de gráfico que pode traduzir as diferenças de potencial elétrico, 𝑈, nos terminais das pilhas X e Y, em função da corrente elétrica, 𝐼, fornecida, é:
Notas:
⇒ A curva característica de uma pilha é dada pela expressão:
- 𝑈 = 𝜀 − 𝑟 𝐼
⇒ Quando uma pilha é utilizada para alimentar um circuito elétrico durante um intervalo de tempo significativo, constata-se que há diminuição da diferença de potencial elétrico nos seus terminais (numericamente igual à ordenada na origem da curva característica) e aumento da sua resistência interna (numericamente igual ao simétrico do declive da curva característica).
- Opção (A) ……………. 10 pontos
10. (2021 – EE) Na Figura 7, está esquematizado um circuito elétrico com os seguintes componentes:
• uma pilha, de força eletromotriz 9,0 V e resistência interna 1,5 Ω;
• três componentes puramente resistivos (R1, R2 e R3), com a mesma resistência elétrica;
• um amperímetro ideal;
• um interruptor.

10.1. Qual a diferença de potencial elétrico entre os pontos P e Q quando o interruptor está aberto?
⇒ Quando o interruptor está aberto, a diferença de potencial lida num voltímetro ligado aos pontos P e Q é igual à diferença de potencial entre os terminais da pilha, isto é, igual à sua força eletromotriz:
- UPilha = ε – ri I ⇔ UPilha = ε
⇒ Assim, a diferença de potencial referida é igual a 9,0 V.
- Apresenta o valor solicitado (9,0 V).
Nota ‒ A ausência de unidade não implica qualquer desvalorização.
10.2. Com o interruptor fechado, o amperímetro regista 0,25 A.
Determine a potência total dissipada nos três componentes puramente resistivos.
Apresente todos os cálculos efetuados.
⇒ O amperímetro está ligado a R3, regista 0,25 A.
⇒ R2 e R3 (iguais) estão ligadas em paralelo, então a corrente elétrica que atravessa R2 também é igual a 0,25 A.
⇒ R1 está ligada em série com R2 e R3, a corrente que a atravessa é igual a 0,50 A (0,25 A + 0,25 A), logo a corrente debitada pela pilha para o circuito é igual a 0,50 A.
⇒ A potência dissipada em R1, R2 e R3 é igual à potência debitada pela pilha ao circuito:
- UPilha = ε – ri I ⇔ UPilha = 9,0 – 1,5 x 0,50 = 8,25 V
- PPilha = UPilha I ⇔ PPilha = 8,25 x 0,5 = 4,1 W
⇒ A potência dissipada nos três componentes, R1, R2 e R3, é igual a 4,1 W.
- Determina o valor solicitado, percorrendo as etapas seguintes:
⇒ Calcula a corrente elétrica fornecida pela pilha (0,50 A) …….. 3 pontos
⇒ Calcula a diferença de potencial elétrico nos terminais da pilha (8,25 V) …….. 4 pontos
⇒ Calcula a potência total dissipada nos três componentes puramente resistivos (4,1 W) …….. 3 pontos
11. (2022 – 1ªF) Com o objetivo de determinar as características de uma pilha, um grupo de alunos montou um circuito elétrico, constituído por uma pilha, uma resistência variável e um interruptor.
Foram também instalados dois aparelhos de medida (um voltímetro e um amperímetro), tal como se esquematiza na Figura 7.
11.1. O voltímetro é o aparelho de medida representado por
(A) X e está instalado em paralelo com a pilha.
(B) X e está instalado em série com a pilha.
(C) Y e está instalado em paralelo com a pilha.
(D) Y e está instalado em série com a pilha.
A pontuação obtida na resposta contribui obrigatoriamente para a classificação final da prova.
- Opção (A) ……………. 10 pontos
11.2. A força eletromotriz da pilha pode ser determinada antes da montagem do circuito, através de uma única medição direta.
Descreva esse procedimento e explique o seu fundamento.
A pontuação obtida na resposta contribui obrigatoriamente para a classificação final da prova.
⇒ A força eletromotriz da pilha pode ser determinada instalando (em série) um voltímetro, X, nos seus terminais, conforme se ilustra na figura, e fazendo a leitura do valor no voltímetro — uma medição direta.
⇒ A força eletromotriz é a diferença de potencial elétrico nos terminais da pilha em circuito aberto.
⇒ Como a resistência interna do voltímetro é muito elevada (há voltímetros com uma resistência interna de aproximadamente 10 MΩ) quando comparada com a resistência interna da pilha de 9 V, o valor da corrente elétrica que percorre o circuito assim constituído é muito baixa, 𝐼 ≈ 0 A (uma corrente elétrica de aproximadamente 1 μA é desprezável quando comparada com os valores apresentados na tabela do item 7.3.).
⇒ Como a diferença de potencial elétrico nos terminais de uma pilha é dada pela expressão 𝑈 = 𝜀−𝑟 𝐼, nessas condições 𝑈 ≈ 𝜀.
⇒ Assim, o valor lido diretamente nos terminais do voltímetro constitui uma boa aproximação para a força eletromotriz da pilha.
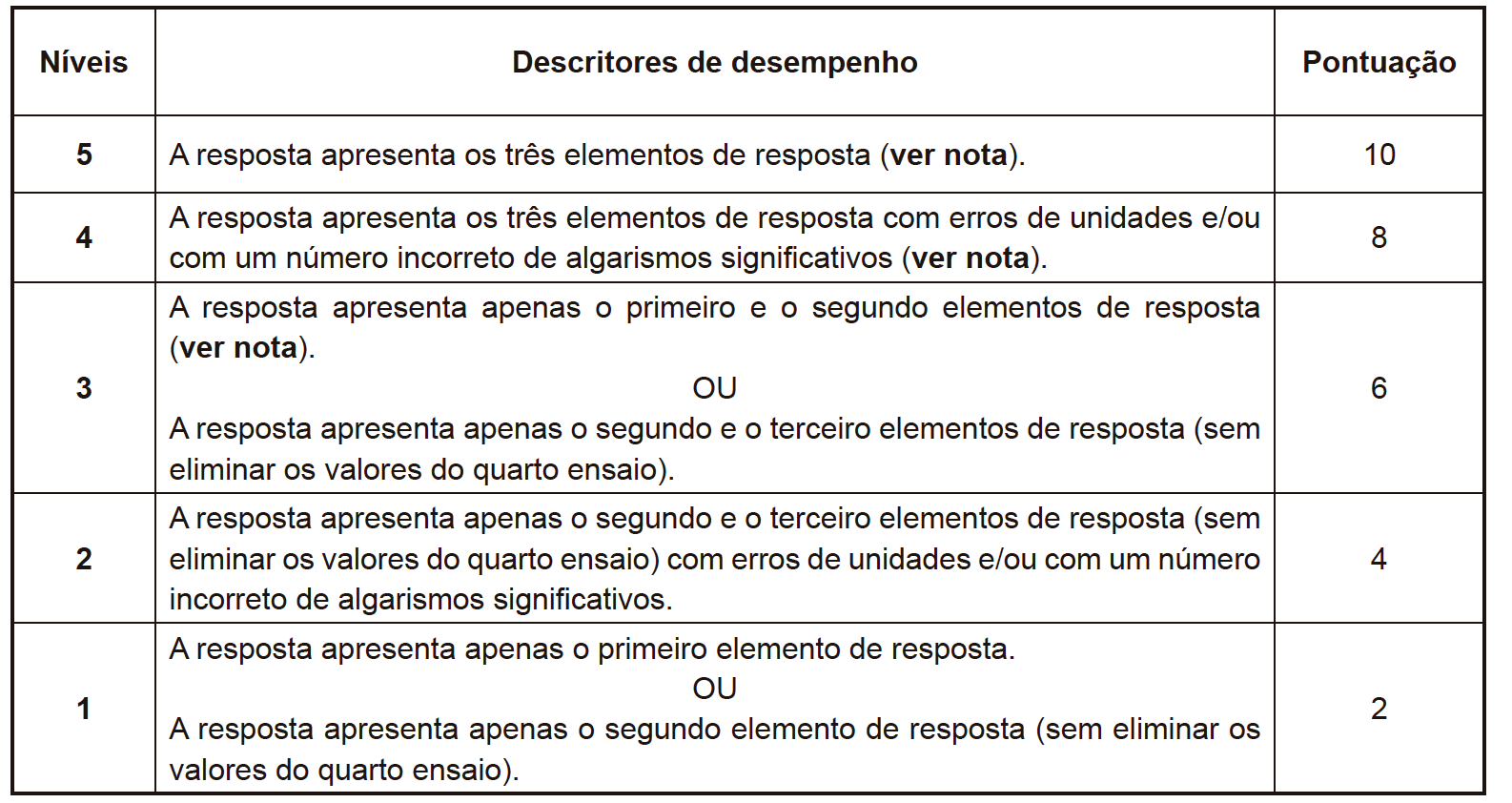
11.3. Na tabela seguinte, estão registados os valores da diferença de potencial, U, e da corrente elétrica, I, medidos para cada valor de resistência elétrica introduzida no circuito.
Ao traçar o gráfico de U, em função de I, os alunos perceberam que um dos pares de valores experimentais não acompanhava a tendência linear dos restantes. Na determinação das características da pilha, decidiram eliminar esse par de valores.
Apresente as características da pilha, com dois algarismos significativos.
Na resposta:
– identifique o par de valores experimentais que os alunos eliminaram;
– apresente a equação da reta de ajuste ao gráfico de U, em função de I (para os cinco ensaios considerados).
A pontuação obtida na resposta contribui obrigatoriamente para a classificação final da prova.
⇒ O gráfico correspondente aos seis ensaios:
Pelo gráfico, podemos verificar que o ensaio que deve ser eliminado é o 4.º, ao qual corresponde o par de valores (0,38 A;6,01 V), que se afasta da relação linear encontrada.
⇒ O gráfico correspondente aos 1.º, 2.º, 3.º, 5.º e 6.º ensaios:
⇒ Características da pilha:
As características de uma pilha são: a força eletromotriz (diferença de potencial elétrico nos terminais da pilha em circuito aberto) e a resistência interna.
A diferença de potencial elétrico nos terminais da pilha é dada por:
- 𝑈 = 𝜀−𝑟 𝐼 ⇔ 𝑈 = 8,91 − 4,3 𝐼 (SI)
Assim,
- 𝜀 = 8,9 V (com dois algarismos significativos, conforme o solicitado)
- 𝑟 = 4,3 Ω
- Elementos de resposta:
⇒ identifica o ensaio a eliminar (4.º ensaio);
⇒ apresenta a equação da reta de ajuste ao gráfico U = f (I) ( U = -4,3 I + 8,9 (V) );
⇒ apresenta a força eletromotriz e a resistência interna da pilha (ε = 8,9 V e ri = 4,3 Ω).
Nota :
- Caso seja apresentada a equação da reta de ajuste ao gráfico U = f (I) correta, considera-se que o primeiro elemento de resposta está presente.
12. (2022 – 2ªF) Na Figura 5, está esquematizado um processo laboratorial destinado a estudar o aquecimento de uma amostra de água.
Montou-se um circuito elétrico com uma pilha, um interruptor e uma resistência de imersão, R.
Neste circuito, foram instalados dois aparelhos de medida, um voltímetro e um amperímetro.
Num ensaio, foi aquecida uma amostra de água durante 10 minutos, usando-se uma resistência elétrica de imersão.
Mediu-se a diferença de potencial, U, de 8,17 V nos terminais da resistência e a corrente elétrica, I, de 700 mA no circuito.
Admita que estes valores se mantiveram constantes ao longo do ensaio.
Qual a energia dissipada pela resistência, por efeito Joule, durante este ensaio?
(A) 4,9 kJ
(B) 3,4 kJ
(C) 1,7 kJ
(D) 5,7 kJ
A pontuação obtida na resposta contribui obrigatoriamente para a classificação final da prova.
- Opção (B)
- Δt = 10 min = 600 s
- U = 8,17 J
- I = 700 mA = 0,700 A
⇒ Edissipada = U I Δt ⇔ Edissipada = 8,17 x 0,700 x 600 ⇔ Edissipada = 3,4 kJ
- Opção (B) ……………. 10 pontos
13. (2022 – EE) No âmbito da agricultura inteligente (ou smart farming), aposta-se na hidroponia, uma técnica de cultivo de espécies vegetais que não necessita de solo e em que se usam ferramentas tecnológicas.
Esta forma de cultivo mais sustentável pode ser implantada em meio urbano, permite economizar água e reforça a segurança alimentar.
No processo de fotossíntese, as plantas não necessitam de absorver radiação em todo o espectro da luz visível.
A clorofila a, nos cloroplastos das plantas, absorve fundamentalmente radiação com comprimentos de onda de 430 nm e de 660 nm.
Em hidroponia, utilizam-se circuitos com associações de vários LED, que emitem, cada um deles, radiação com um dos comprimentos de onda referidos anteriormente.
Na Figura 6, representam-se curvas características de dois tipos de LED, X e Y, que poderão ser utilizados em iluminação em estações hidropónicas.

Para testar a adequação de dois LED, 1 e 2, montou-se um circuito elétrico no qual estes foram associados em paralelo com uma pilha ideal (de resistência interna nula) de força eletromotriz 9,0 V.
O circuito elétrico inclui ainda um aparelho de medida (amperímetro) e duas resistências elétricas, R e outra, de 360 X, de acordo com a Figura 7.
Para preservar a longevidade e o bom funcionamento dos LED, a corrente elétrica que atravessa cada LED não pode exceder 20 mA.
Dada esta condição, para uma corrente elétrica de 40 mA, lida no amperímetro, o valor de R é
(A) 280 X, e o LED 2 corresponde ao LED Y da Figura 6.
(B) 225 X, e o LED 2 corresponde ao LED Y da Figura 6.
(C) 280 X, e o LED 2 corresponde ao LED X da Figura 6.
(D) 225 X, e o LED 2 corresponde ao LED X da Figura 6.
A pontuação obtida na resposta contribui obrigatoriamente para a classificação final da prova.
- Opção (A) ……………. 10 pontos