Voltar a: Atividades Laboratoriais – 11ºAno
Questões práticas
- Al 1.1 – Queda livre: força gravítica e aceleração da gravidade;
1. Uma esfera foi abandonada imediatamente acima da célula fotoelétrica 1 e, com um digitímetro associado a uma célula fotoelétrica, os alunos registaram o tempo de passagem da esfera na célula fotoelétrica 2 .
Este procedimento foi repetido três vezes, os alunos mediram o tempo de passagem da esfera entre a célula 1 e a célula 2.
Os resultados das medições obtidas estão registados na tabela seguinte:
Apresenta o valor mais provável para o tempo de queda, acompanhado pela respetiva incerteza absoluta.
(A) 11,04 ms ± 5,98 %
(B) 11,04 ms ± 6,0 %
(C) 11,04 ms ± 0,60 %
(D) 11,04 ms ± 0,6 %
- Opção (B)
🟢 O valor mais provável é a média:
- o maior desvio 0,66 s
🟢 A incerteza relativa é dada por:
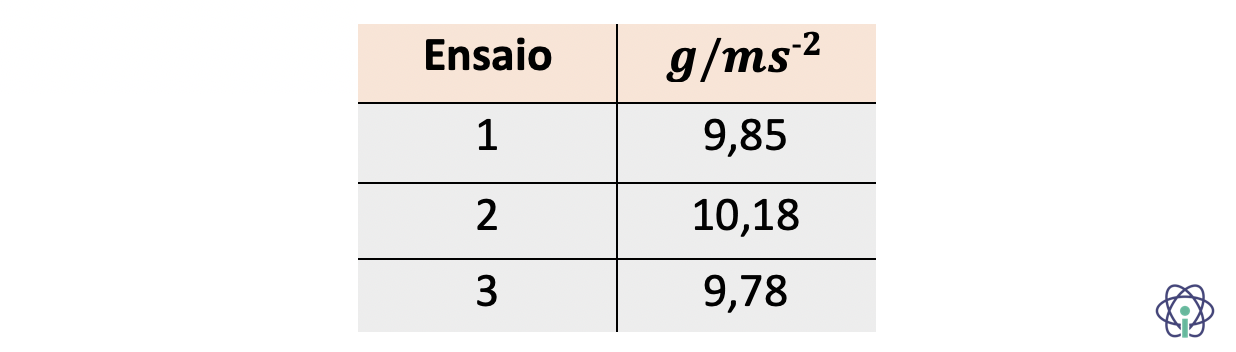
2. Para calcular a aceleração da gravidade um grupo de alunos realizou três ensaios nas mesmas condições.
Os resultados encontram-se registados na tabela seguinte.
Calcula a aceleração da gravidade da medição, em função do valor mais provável e da incerteza absoluta.
Apresenta todas as etapas de resolução.
🟢 Cálculo do valor mais provável da aceleração da gravidade:
🟢 Determinação dos módulos dos desvios de cada valor medido em relação ao valor mais provável:
🟢 Resultado da medição do valor da aceleração da gravidade:
- g = ( 9,94 ± 0,24 ) m s-2
3. Para realizar uma atividade experimental de queda livre, um grupo de alunos, usaram uma medalha de 168,0 g e 152,8 mm de diâmetro e um berlinde de 66,0 g e 40,0 mm de diâmetro.
Escreve o valor do diâmetro e da massa de cada um dos corpos, tendo em consideração o valor da incerteza absoluta de leitura.
➩ mmedalha = ( 168,0 ± 0,1 ) g
➩ dmedalha = ( 152,8 ± 0,1 ) mm
➩ mberlinde = ( 66,0 ± 0,1 ) g
➩ dberlinde = ( 40,0 ± 0,1 ) mm
4. Para realizar uma atividade experimental de queda livre, um grupo de alunos, usaram uma medalha de 8,0 g e 20 mm de diâmetro.
4.1. Determina o valor da aceleração da gravidade da medalha.
4.2. Determina o erro percentual a ele associado.
Dado: g = 9,80 m s-2
4.1.
4.2.
- g = 9,90 m s-2 ± 1,0 %
5. Para calcular a aceleração da gravidade um grupo de alunos realizou dois ensaios nas mesmas condições.
Os resultados encontram-se registados na tabela seguinte.
Determina o valor mais provável da aceleração da gravidade obtido experimental e o erro percentual a ele associado.
Dado: g = 9,8 m s-2
🟢 Cálculo do valor mais provável da aceleração da gravidade:
🟢 Resultado da medição do valor da aceleração da gravidade:
- g = 9,92 m s-2 ± 1,2 %
6. Para determinar a aceleração da gravidade de uma pequena esfera de diâmetro 18,85 mm, em queda livre, um grupo de alunos utilizou uma montagem experimental que incluía duas células fotoelétricas ligadas a um marcador de tempo digital.
A tabela seguinte resume os valores experimentais obtidos por os alunos.
Dado: g = 9,80 m s-2
6.1. Apresenta, para esse conjunto de ensaios, o resultado da medição de Δt em função da respetiva incerteza absoluta ou da respetiva incerteza relativa em percentagem.
6.2. Calcula o módulo da velocidade de passagem da esfera em cada uma das células fotoelétricas.
6.3. Determina valor experimental do módulo da aceleração da esfera em queda livre.
6.4. Analisa a exatidão associada ao valor da aceleração obtido, determinando o erro relativo percentual.
6.1.
6.2.
🟢 O intervalo de tempo associado à passagem da esfera pelo feixe da célula fotoelétrica é extremamente reduzido, pelo que a variação do módulo da velocidade nesse intervalo de tempo também será muito pequena.
🟢 O módulo da velocidade pode considerar-se aproximadamente constante e, portanto, equivalente ao valor da velocidade média nesse intervalo de tempo, podendo aplicar-se a expressão
6.3.
6.4.
O erro relativo em percentagem pode ser determinado pela expressão:
Uma vez que o valor do erro relativo obtido para a esfera é relativamente reduzido, pode considerar-se que o resultado é bastante exato.
7. Uma esfera foi abandonada imediatamente acima da célula fotoelétrica 1 e, com um digitímetro associado a uma célula fotoelétrica, os alunos registaram o tempo de passagem da esfera na célula fotoelétrica 2 .
Este procedimento foi repetido três vezes, os alunos mediram o tempo de passagem da esfera entre a célula 1 e a célula 2.
Os resultados das medições obtidas estão registados na tabela seguinte:
Apresenta o valor mais provável para o tempo de queda, acompanhado pela respetiva incerteza absoluta.
🟢 O valor mais provável é a média:
- o maior desvio 0,013 s
🟢 Resultado da medição é:
- Δt1→2 = ( 0,369 ± 0,013 ) s
8. Para realizar uma atividade experimental de queda livre, um grupo de alunos, usaram um berlinde de 26,0 g e 28,0 mm de diâmetro.
8.1. Determina o valor da aceleração da gravidade do berlinde.
8.2. Determina o erro percentual a ele associado.
Dado: g = 9,80 m s-2
8.1.
8.2.
- g = 9,64 m s-2 ± 1,7 %
9. Obteve-se um valor experimental para o módulo da aceleração gravítica com 6,50 % de erro, por excesso.
Considerando que o tempo médio de passagem pela célula B foi de 9,89 ms e o tempo médio decorrido desde a célula A até à B foi de 278 ms, determina o diâmetro da esfera usada.
Apresenta todas as etapas de resolução, explicitando todos os cálculos efetuados.
Dado: g = 9,80 m s-2
10. (2010 – 2ªF) Para investigar se o valor da aceleração da gravidade depende da massa dos corpos em queda livre e da altura de queda, um grupo de alunos usou duas células fotoelétricas, X e Y, ligadas a um cronómetro digital, e diversas esferas de um mesmo material, mas com diâmetros diferentes.
A Figura 5 representa um esquema da montagem utilizada.
Os alunos começaram por medir, com uma craveira, o diâmetro, d, de cada uma das esferas.
Realizaram, seguidamente, diversos ensaios, para determinarem:
– o tempo que cada esfera demora a percorrer a distância entre as células X e Y, Δtqueda ;
– o tempo que cada esfera demora a passar em frente à célula Y, ΔtY.
Os alunos tiveram o cuidado de largar cada esfera sempre da mesma posição inicial, situada imediatamente acima da célula X, de modo a poderem considerar nula a velocidade com que a esfera passava nessa célula (vX = 0).
10.1. Para uma dada esfera, os alunos obtiveram os valores mais prováveis do diâmetro, d, e do tempo de passagem da esfera pela célula Y, ΔtY :
• d = 2,860 cm
• ΔtY = 12,3 x 10–3 s
Os alunos usaram a expressão
(que se refere a um movimento retilíneo uniforme) para calcular um valor aproximado da velocidade, vY, com que a esfera passa na célula Y.
10.1.1. Explique por que é possível utilizar-se aquela expressão no cálculo do valor aproximado da velocidade vY.
⇒ O diâmetro da esfera é pequeno e o intervalo de tempo que a esfera demora a passar pela célula fotoelétrica é também pequeno, pelo que se pode afirmar que nesse intervalo de tempo a velocidade da esfera é praticamente constante.
10.1.2. Os alunos obtiveram, em três ensaios consecutivos, os valores de tempo que a esfera demora a percorrer a distância entre as células X e Y, Δtqueda , apresentados na tabela seguinte.
Calcule o valor experimental da aceleração da gravidade obtido pelos alunos a partir das medidas efetuadas.
Apresente todas as etapas de resolução.
⇒ Calculando o valor da velocidade de passagem vem:
⇒ O tempo mais provável que a esfera demorou a adquirir aquela velocidade foi:
⇒ Logo, calculando a aceleração:
10.2. A tabela seguinte apresenta alguns dos valores experimentais da aceleração da gravidade, expressos em ms–2, obtidos pelos alunos, utilizando esferas de massas diferentes e alturas de queda diferentes.
Selecione a única opção que contém os termos que preenchem, sequencialmente, os espaços seguintes, de modo a obter uma afirmação correta.
A partir dos resultados experimentais obtidos, podemos concluir que o valor da aceleração da gravidade ______ da massa dos corpos em queda e que ______ da altura de queda.
(A) depende … depende
(B) depende … não depende
(C) não depende … depende
(D) não depende … não depende
- Opção (D)
⇒ Para as diferentes massas e para diferentes alturas de queda, os valores da aceleração na tabela são aproximadamente os mesmos.
11. (TI – 29/04/2013) A Figura 3 (que não está à escala) representa uma pequena bola, colocada sob um sensor de movimento, e um referencial unidimensional de eixo vertical, Oy.
A bola foi abandonada, caindo no ar até atingir o solo.
A bola foi abandonada, no instante t = 0 s, da posição representada na figura, caindo 1,40 m até ao solo.
A partir dos dados adquiridos com o sensor de movimento, concluiu-se que a componente escalar, segundo o eixo Oy, da posição, y, da bola variava com o tempo, t, de acordo com a equação
y = 0,20 + 5,0 t 2 (SI)
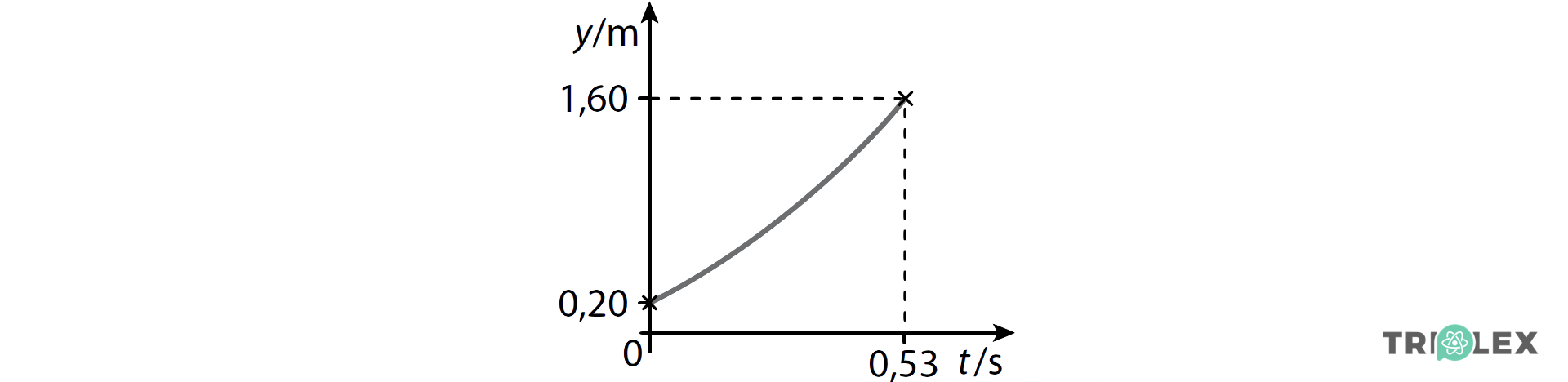
11.1 Apresente o gráfico da componente escalar da posição, y, da bola em função do tempo, t , desde o instante em que a bola foi abandonada até ao instante em que atingiu o solo.
Utilize a calculadora gráfica.
Na sua resposta, deve reproduzir o gráfico obtido com a calculadora, no intervalo de tempo considerado, indicando no gráfico:
• as grandezas representadas e as respetivas unidades;
• as coordenadas dos pontos que correspondem ao instante em que a bola foi abandonada e ao instante em que a bola atingiu o solo.
⇒ Antes de recorrer à calculadora gráfica, determina-se analiticamente a posição inicial da bola em relação à origem do referencial (sensor), y0, a sua posição ao atingir o solo, ys, e o tempo de queda, ts, de modo a conseguir visualizar na janela da calculadora o gráfico y = f(t).
- y = 0,20 + 5,0 t2 (SI)
⇒ Para t = 0 s, y0 = 0,20 m;
⇒ Como ys – y0 = 1,40 m, então, ys – 0,20 = 1,40 ⇔ ys = 1,60 m;
⇒ Para ys = 1,60 m, tem-se 1,60 = 0,20 + 5,0 t2 ⇔ t = 0,53 s
11.2 Que distância percorreu a bola desde o instante em que foi abandonada até ao instante t = 0,30 s?
(A) 0,85 m
(B) 0,75 m
(C) 0,65 m
(D) 0,45 m
- Opção (D)
⇒ A distância percorrida até t = 0,30 s é d = |y – 0,20|
- d = 5,0 x 0,302 = 0,45 m
11.3 Explique porque é que se pode admitir que a força de resistência do ar não influenciou o movimento de queda da bola.
⇒ Comparando a equação do movimento da bola, y = 0,20 + 5,0 t2, com a equação y = y0 + ½ a t2, constata-se que a aceleração de queda é de 10 m s-2, pois ½ a = 5,0 m s– 2, igual ao módulo da aceleração gravítica, g, de um corpo junto à superfície terrestre (ver Tabela de Constantes).
⇒ De acordo com a 2.ª Lei de Newton, Fr = m a , o valor da aceleração adquirida por um corpo é diretamente proporcional à intensidade da resultante das forças que sobre ele atuam.
⇒ Como a = g e considerando-se que sobre a bola apenas atuam a força gravítica, Fg = m g, e a resistência do ar, conclui-se que esta força não influenciou o movimento de queda da bola, pois a força resultante é igual à gravítica.
12. (2017 – 1ªF) A Figura 3 representa uma montagem que foi utilizada na determinação experimental do módulo da aceleração gravítica.
Nos vários ensaios realizados, abandonou-se uma esfera sempre da mesma posição inicial, imediatamente acima da célula fotoelétrica A.
Numa primeira experiência, mantendo as células fotoelétricas à mesma distância uma da outra, mediu-se o tempo que a esfera demorou a percorrer a distância entre as células A e B, tA→B, e o tempo que a esfera demorou a passar em frente da célula B, tB.
12.1. Num conjunto de ensaios, realizados nas mesmas condições, obtiveram-se os valores de tB apresentados na tabela seguinte.
Qual é, para esse conjunto de ensaios, o resultado da medição de tB?
(A) tB = (8,80 ± 0,01) ms
(B) tB = (8,80 ± 0,06) ms
(C) tB = (8,80 ± 0,05) ms
(D) tB = (8,80 ± 0,04) ms
- Opção (D)
⇒ O valor mais provável do tempo de passagem em B é:
⇒ Os desvios de cada uma das leituras são:
⇒ A incerteza absoluta é igual ao módulo do desvio máximo, desde que superior à incerteza de leitura do cronómetro digital ( 0,01 ms) , ou seja, igual a 0,04 ms
- O resultado da medição é tB = ( 8,80 ± 0,04) ms
12.2. Dividindo o diâmetro da esfera por tB , determina-se um valor aproximado do módulo da velocidade da esfera no instante em que esta se encontra em frente da célula fotoelétrica B, vB.
12.2.1. Ao determinar vB por este método, que aproximação se faz?
⇒ Considera-se que a velocidade da esfera no intervalo de tempo 𝑡B aproximadamente constante (despreza-se a variação de velocidade, porque o intervalo de tempo 𝑡B é muito pequeno).
ou
⇒ Considera-se que a velocidade no instante em que a esfera se encontra em frente da célula é aproximadamente igual à velocidade média no intervalo de tempo 𝑡B.
12.2.2. O cálculo de vB pressupõe que a esfera interrompe o feixe luminoso da célula B pelo seu diâmetro.
No entanto, um erro experimental frequente decorre de a esfera interromper, de facto, o feixe luminoso por uma dimensão inferior ao seu diâmetro.
Quando este erro ocorre, o valor de vB calculado é ______ ao verdadeiro, o que determina um erro por ______ no valor experimental do módulo da aceleração gravítica.
(A) superior … excesso
(B) superior … defeito
(C) inferior … excesso
(D) inferior … defeito
- Opção (A)
⇒ Se o cálculo do valor de vB for feito com o valor do diâmetro da esfera, mas com um valor medido de tB inferior ao valor verdadeiro, fará com que o valor de vB calculado seja superior ao valor verdadeiro.
⇒ O valor experimental do módulo da aceleração gravítica,
- será maior do que o valor verdadeiro, o que determina um erro por excesso.
12.3. No cálculo do módulo da aceleração gravítica, que valor deverá ser considerado para o módulo da velocidade da esfera no instante em que esta se encontra em frente da célula fotoelétrica A?
⇒ Dado que a esfera é abandonada imediatamente acima da célula A e que o módulo da velocidade com que está à frente desta é desprezável em relação ao calculado em B, deve considerar-se esse valor igual a 0 m s–1 .
12.4. Numa segunda experiência, variando a distância entre as células A e B, foi possível determinar o módulo da aceleração gravítica a partir do gráfico do quadrado do tempo que a esfera demorou a percorrer a distância entre as células, t2A→B, em função da distância percorrida, Δy.
A partir dos valores obtidos, determinou-se a equação da reta que melhor se ajusta ao conjunto de pontos do gráfico:
t2A→B = 0,198Δy − 0,001 (SI)
Determine o erro percentual (erro relativo, em percentagem) do módulo da aceleração gravítica obtido nesta experiência, tomando como referência o valor 9,8 m s-2.
Apresente todas as etapas de resolução.
⇒ Como já foi referido, pode considerar-se que a esfera em A parte do repouso.
Assim, pode escrever-se:
⇒ Da equação da reta apresentada no enunciado tem-se:
⇒ O erro relativo percentual é:
- O erro percentual do módulo da aceleração gravítica é 3,1%
