Voltar a: 11ºAno – Física
- Ficha nº5
⇒ Movimentos retilíneos em planos horizontais
1. O Pedro estava a jogar ténis, a uma dada altura a bola foi parar ao terreno do seu vizinho. Quando foi buscar a bola, encontrou o Bob, um cão bastante agressivo.
O Bob, parte do repouso, alcança (com aceleração constante) a velocidade máxima de 60 km h-1 em 4,0 s e é capaz de manter essa velocidade durante mais 10 s.
O Pedro ao fim de 3,0 s apercebe-se do Bob e começa a fugir dele, parte do repouso, alcança (com aceleração constante) a sua velocidade máxima, que é 80% da velocidade máxima do Bob, ao fim de 5,0 s e consegue mantê-la por mais tempo que o bob.
Infelizmente para o Pedro que não consegue evitar que o Bob o apanhe ao fim de 12,0 s depois de o Bob ter iniciado a perseguição.
Considerando que se deslocaram retilíneamente, calcula a distância a que se encontravam quando o Bob iniciou a corrida.
🟡 60 km h-1 = 16,7 m s-1
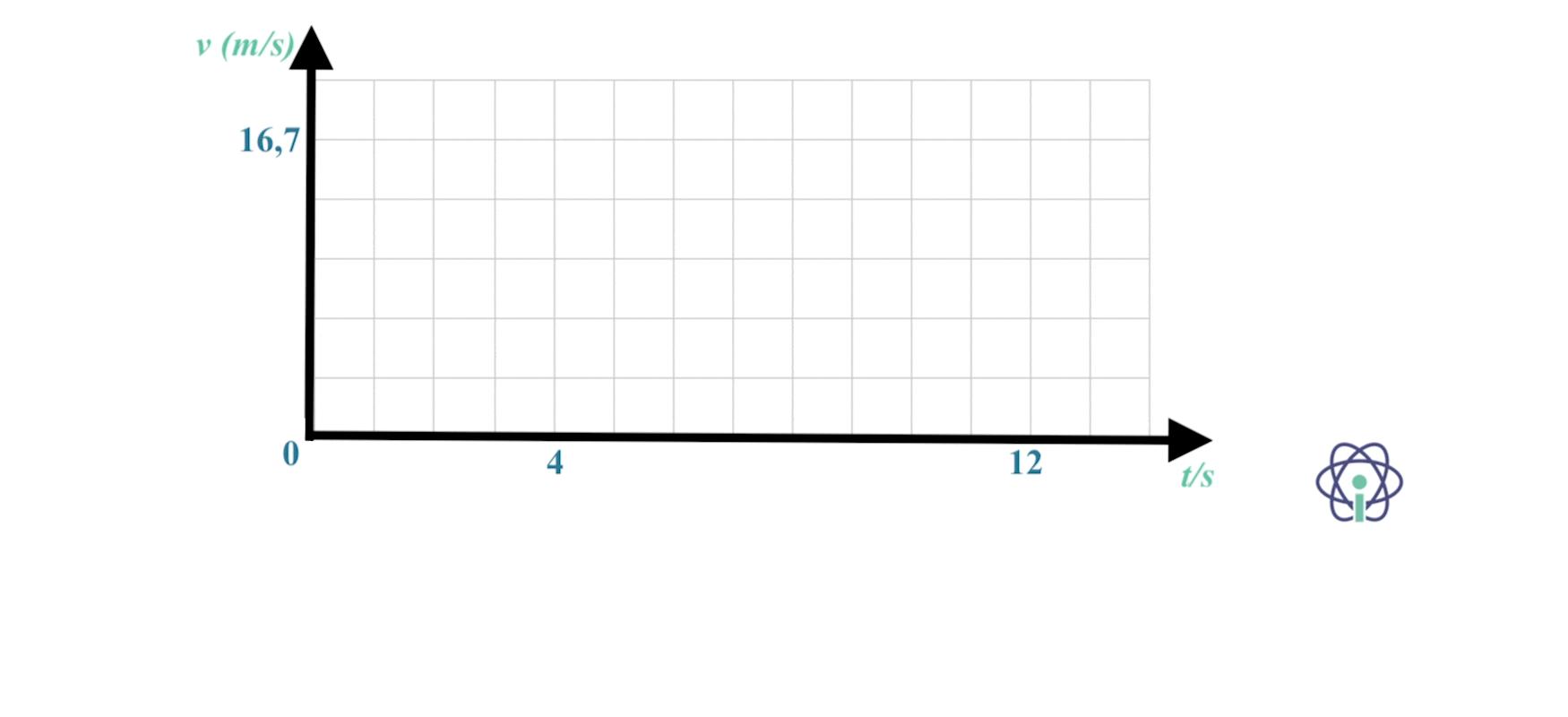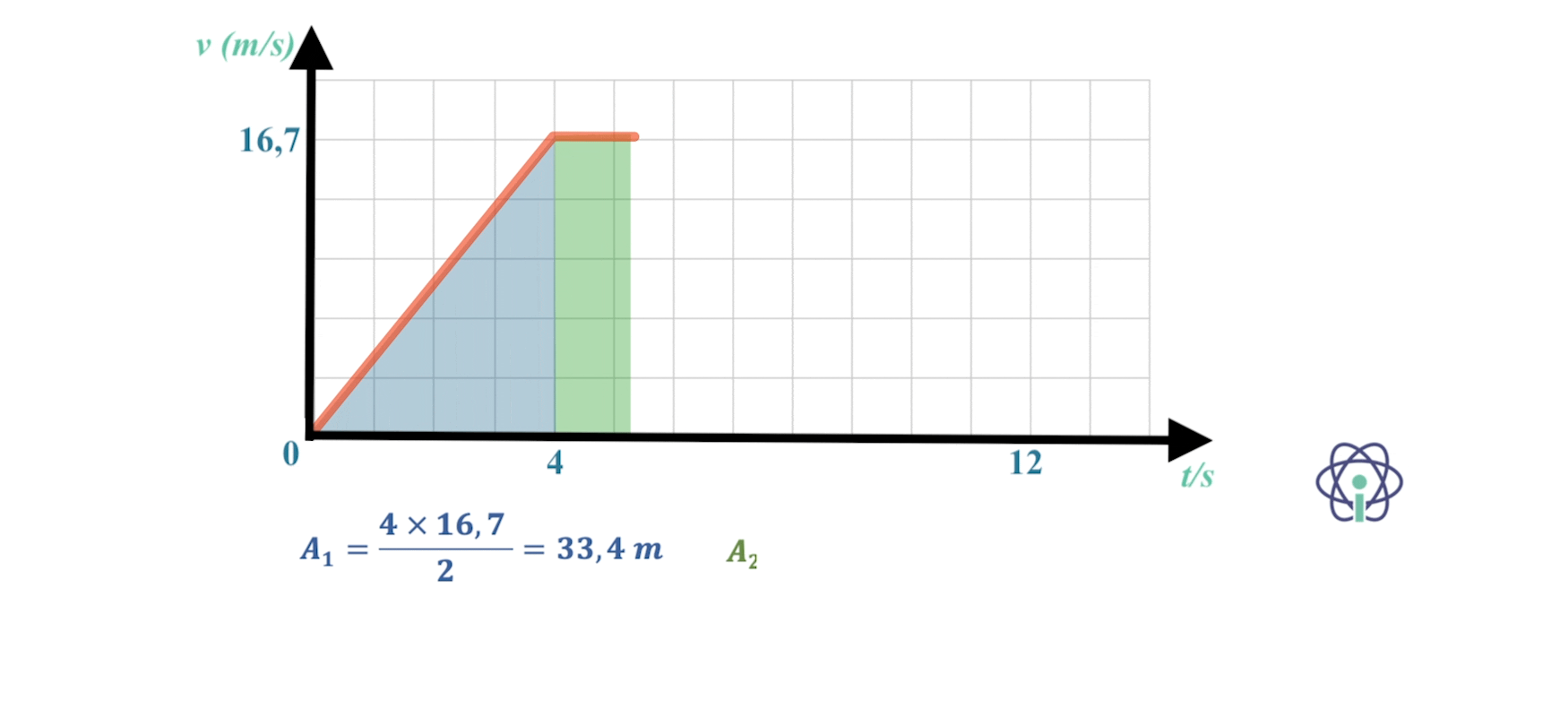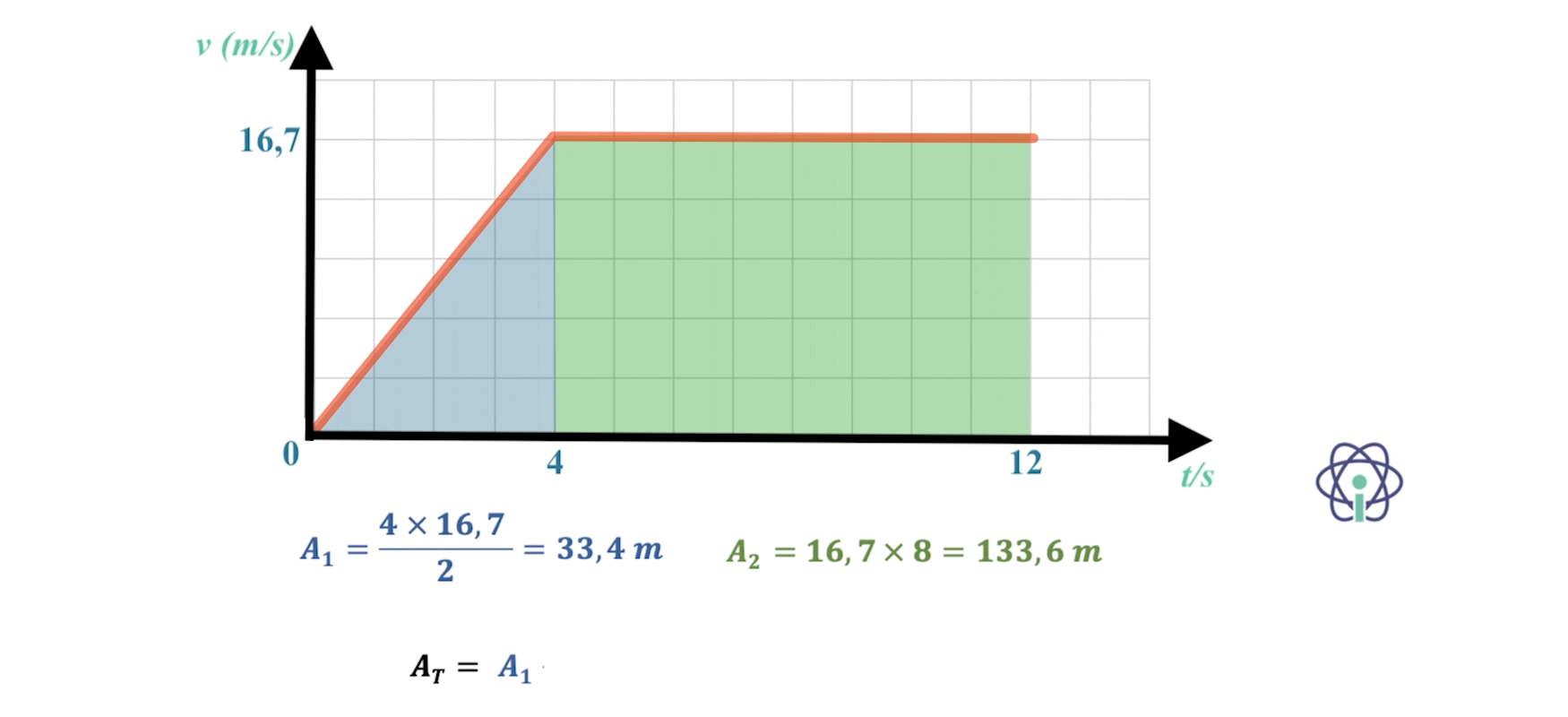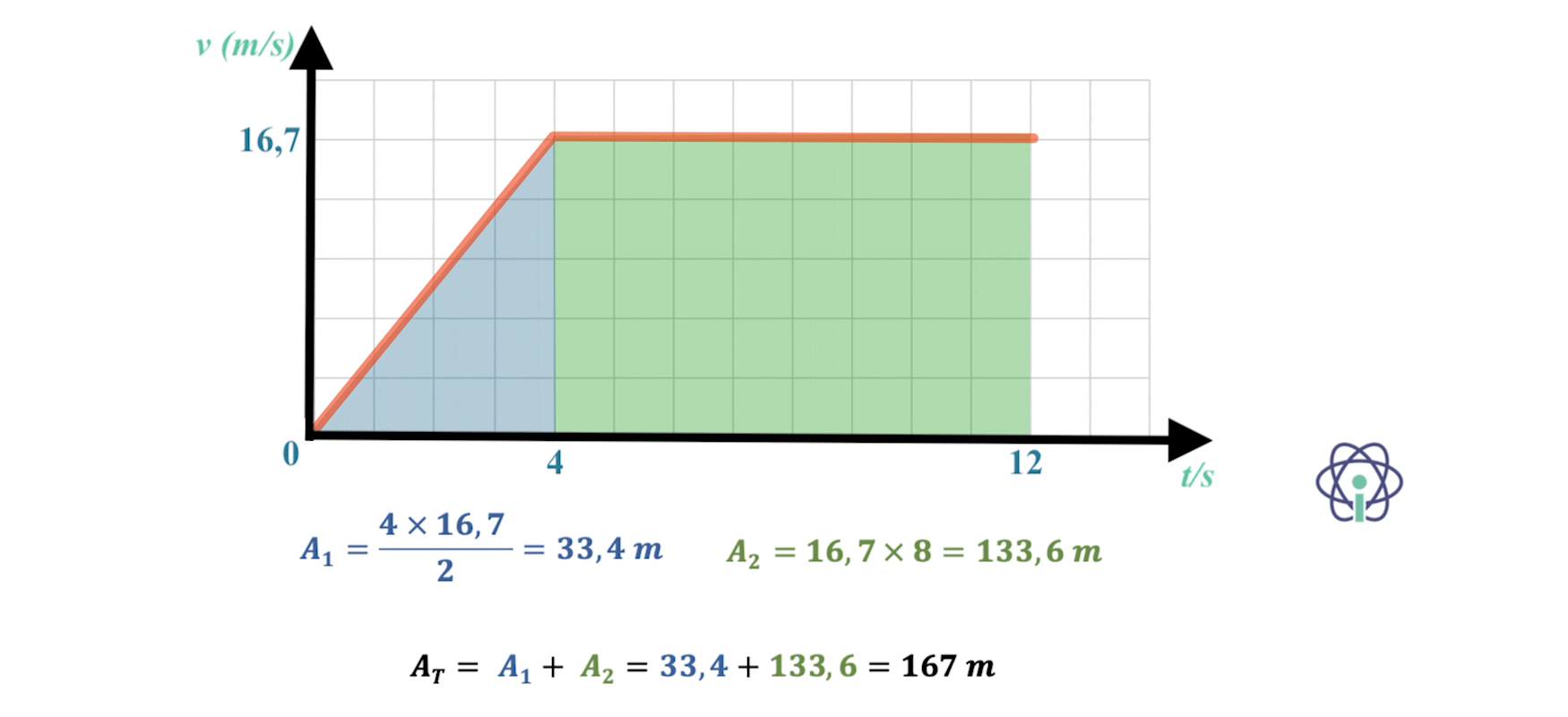
- Bob:
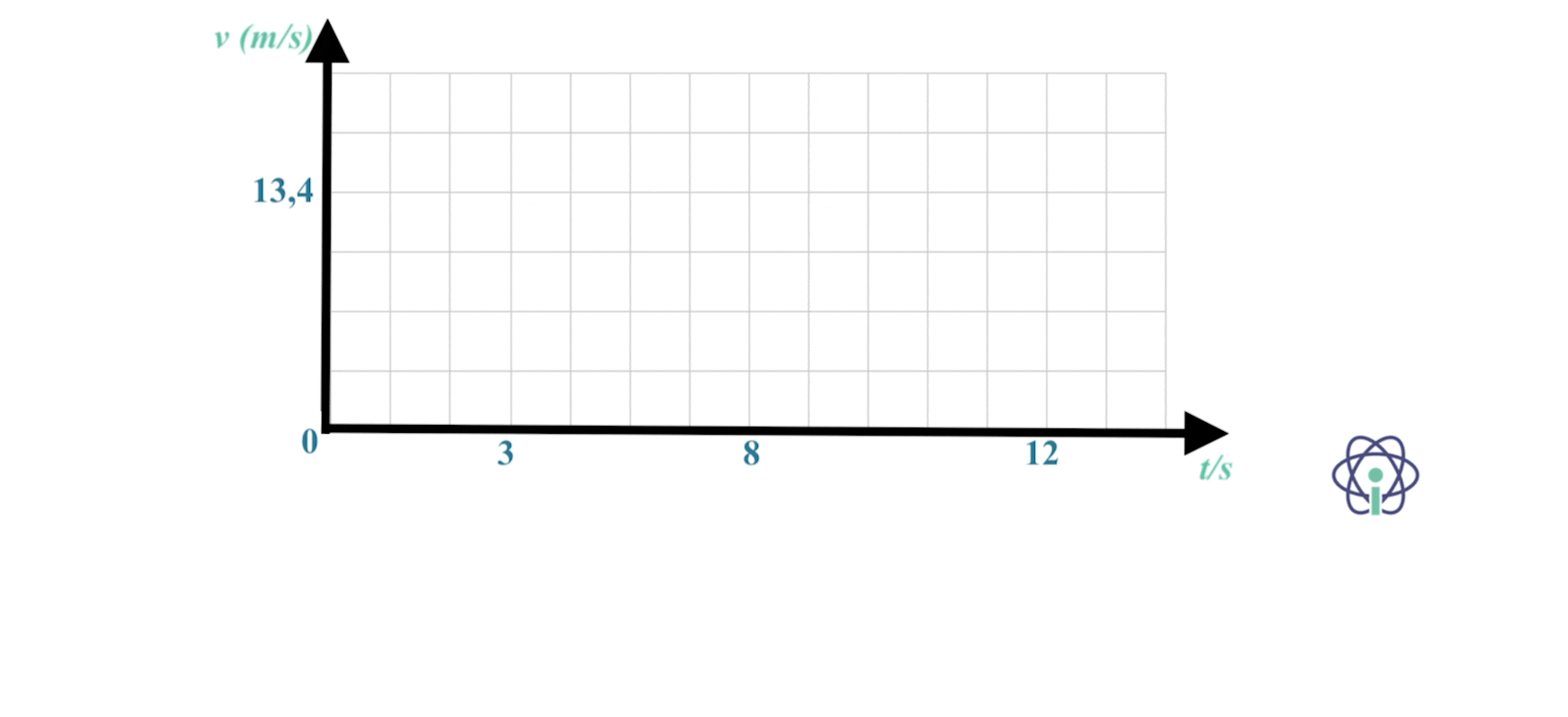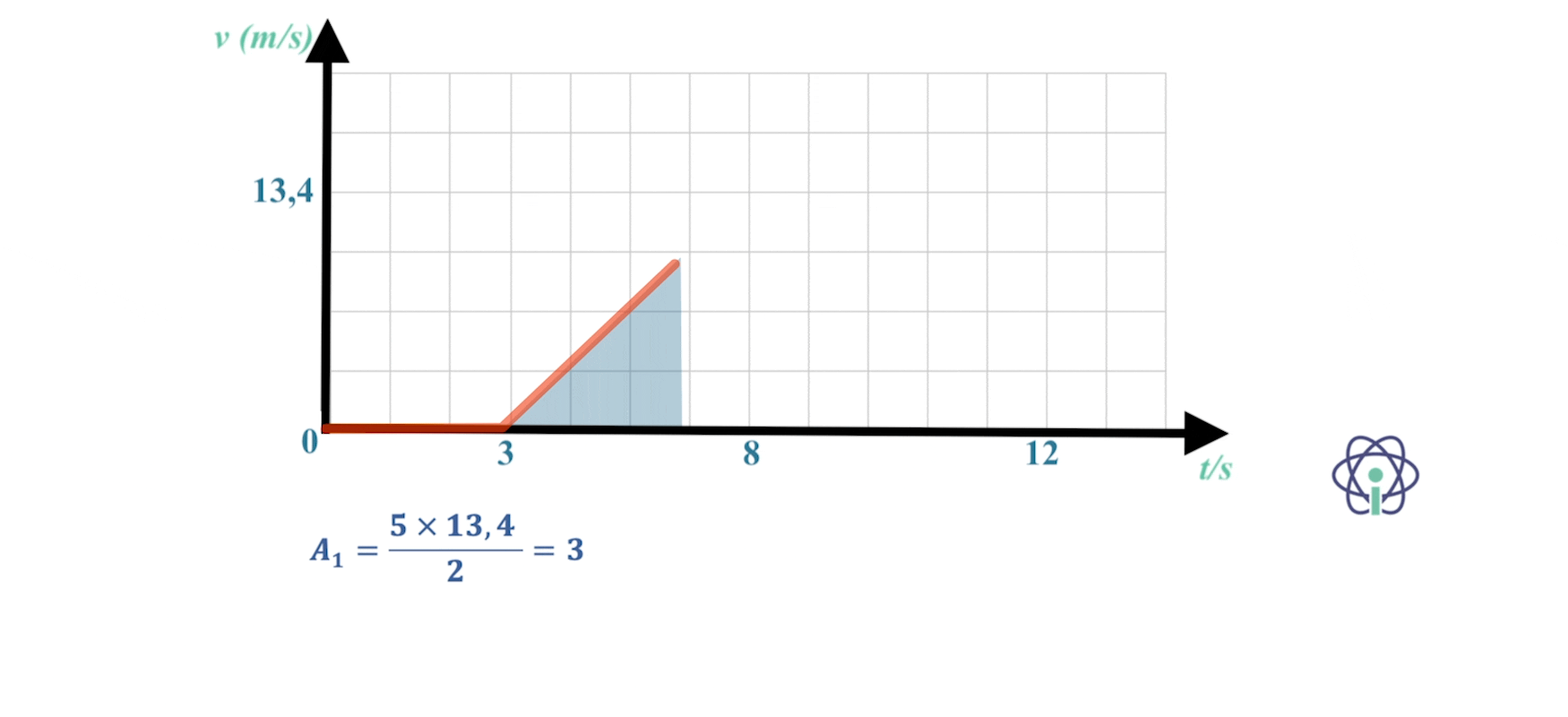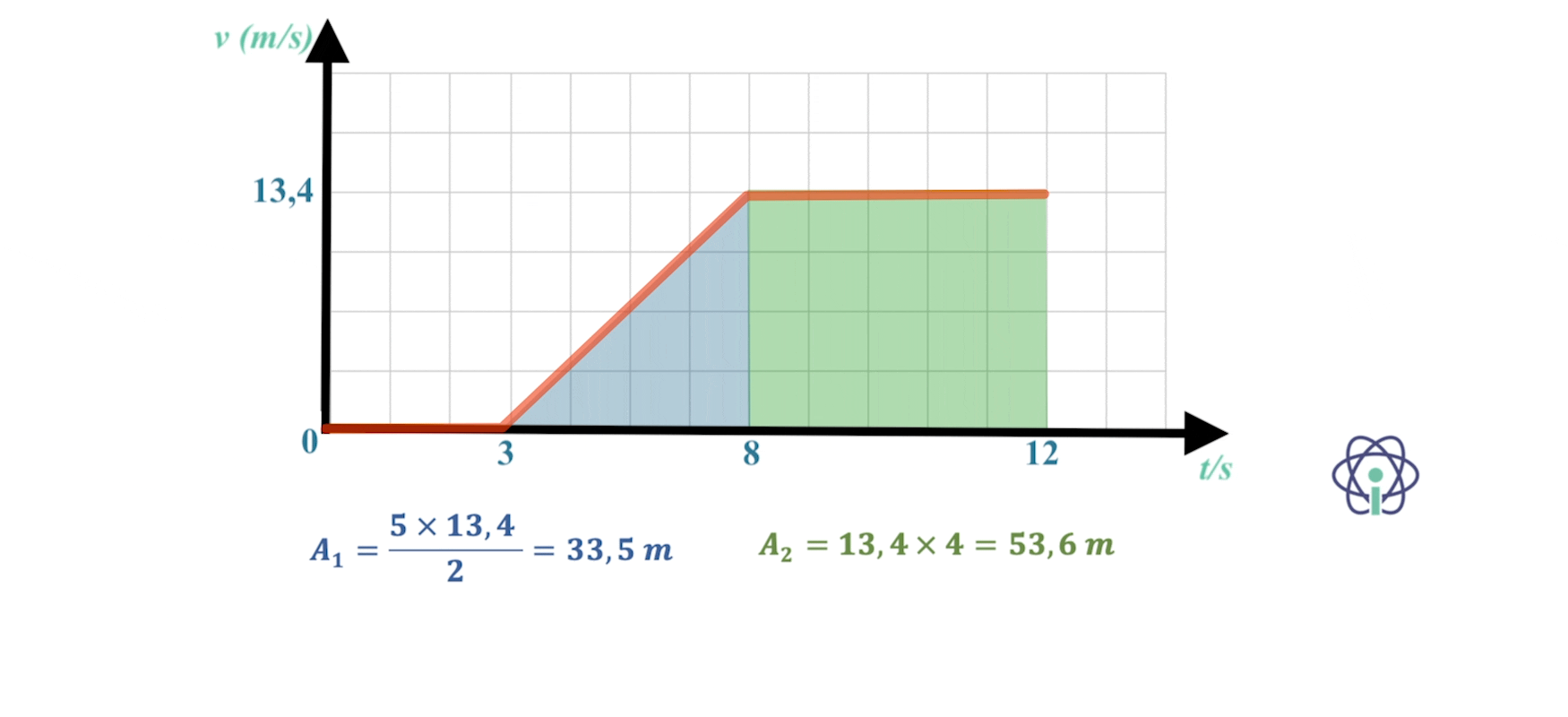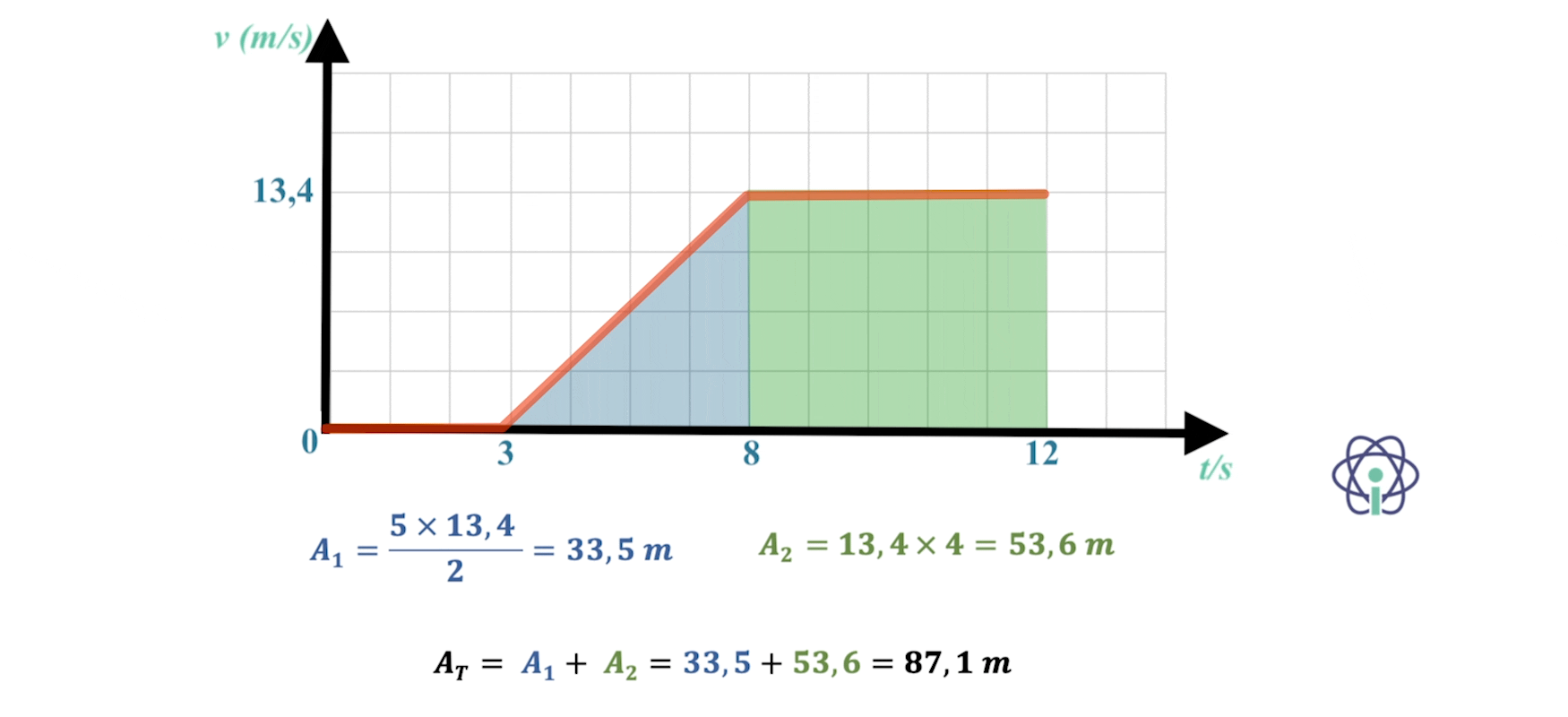
⇒ Durante os 4 s que o Bob correu com movimento uniformemente acelerado percorreu 33,4 m e nos 8 s seguintes, já com movimento uniforme, percorreu mais 133,6 m, totalizando aproximadamente 167 m.
- Pedro
⇒ O Pedro, nos primeiros 5,0 s da sua acorrida, percorreu cerca de 33,5 m, como o Pedro só começou a fugir do Bob 3,0 s depois de este ter iniciado a fuga, apenas fugiu durante 9,0 s, por isso só se deslocou com velocidade constante 4,0 s, nesse intervalo de tempo percorreu cerca de 53 m, no total, o Pedro deslocou-se 87,1 m.
- Conclui-se que, no início, a distância entre os dois era de cerca de 80 m.
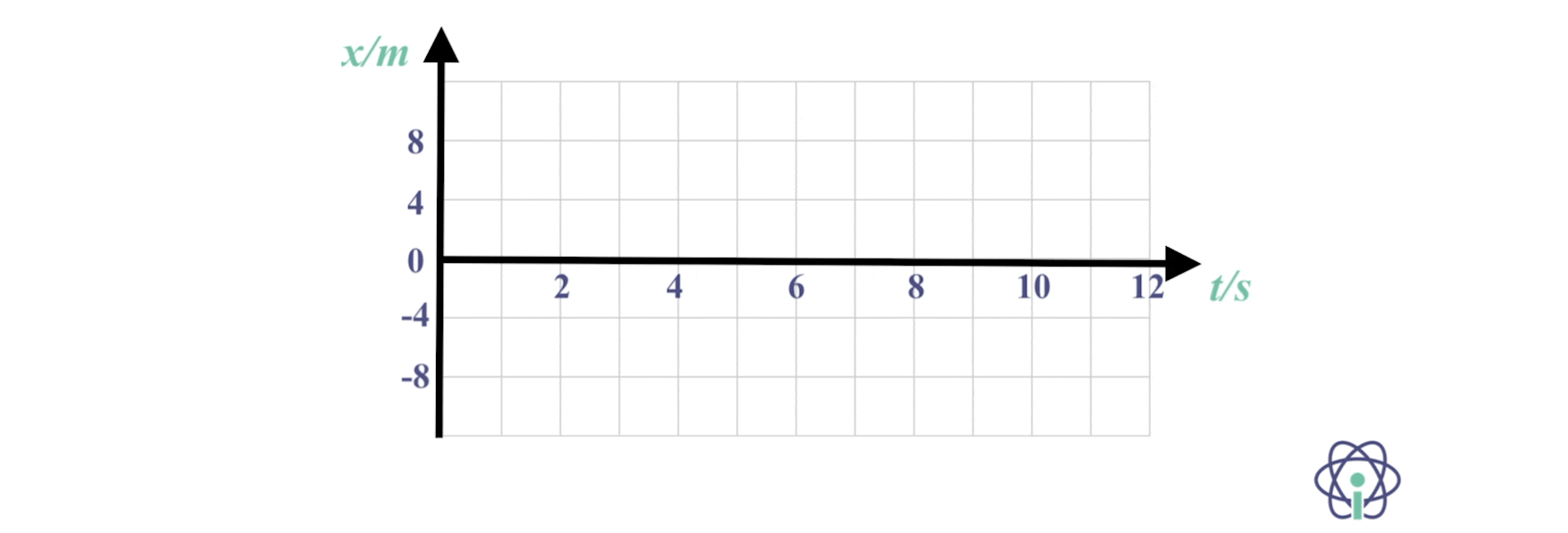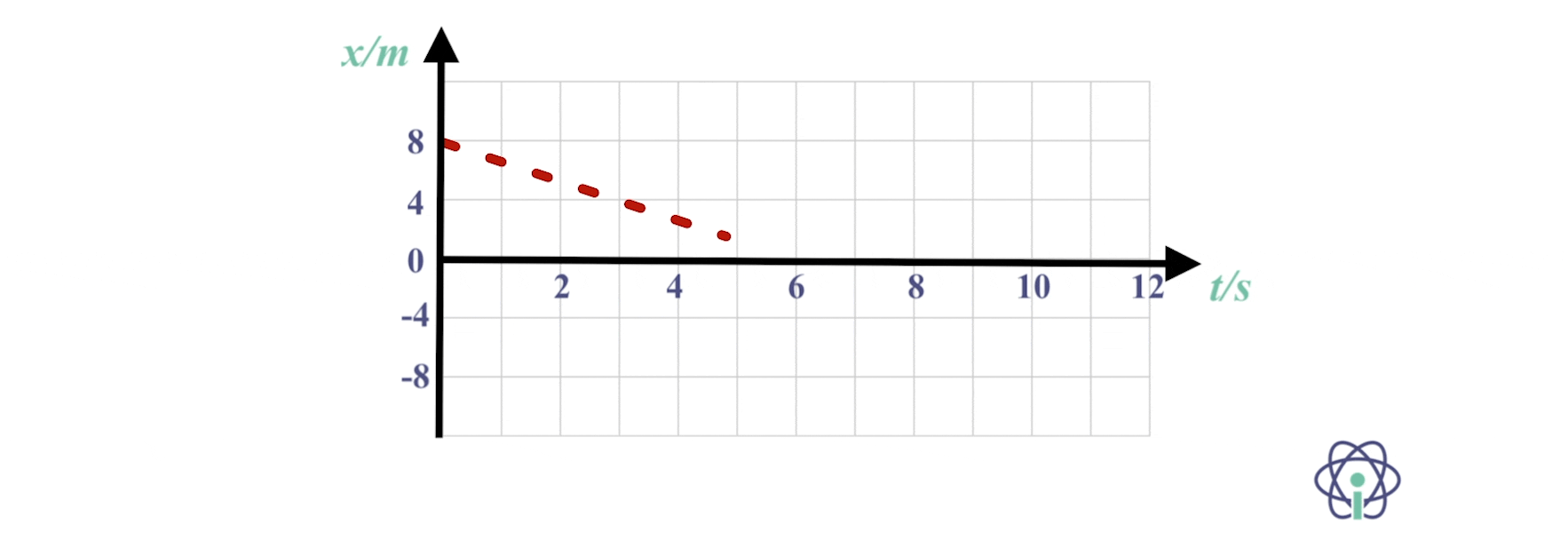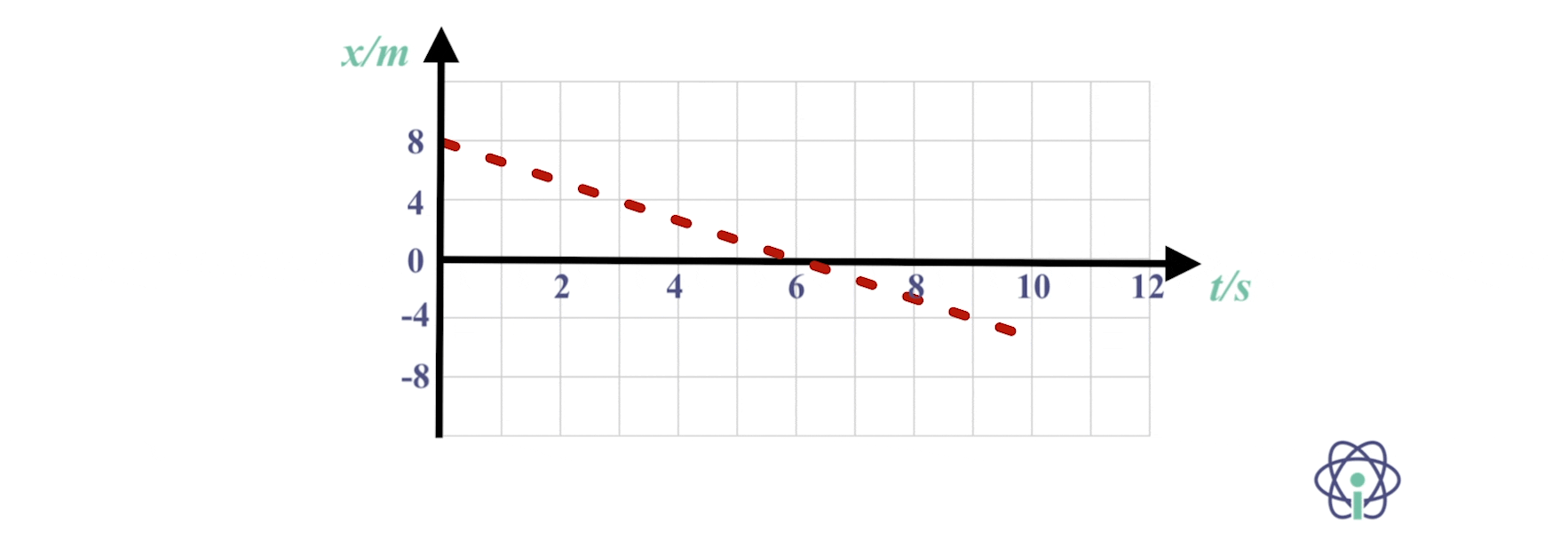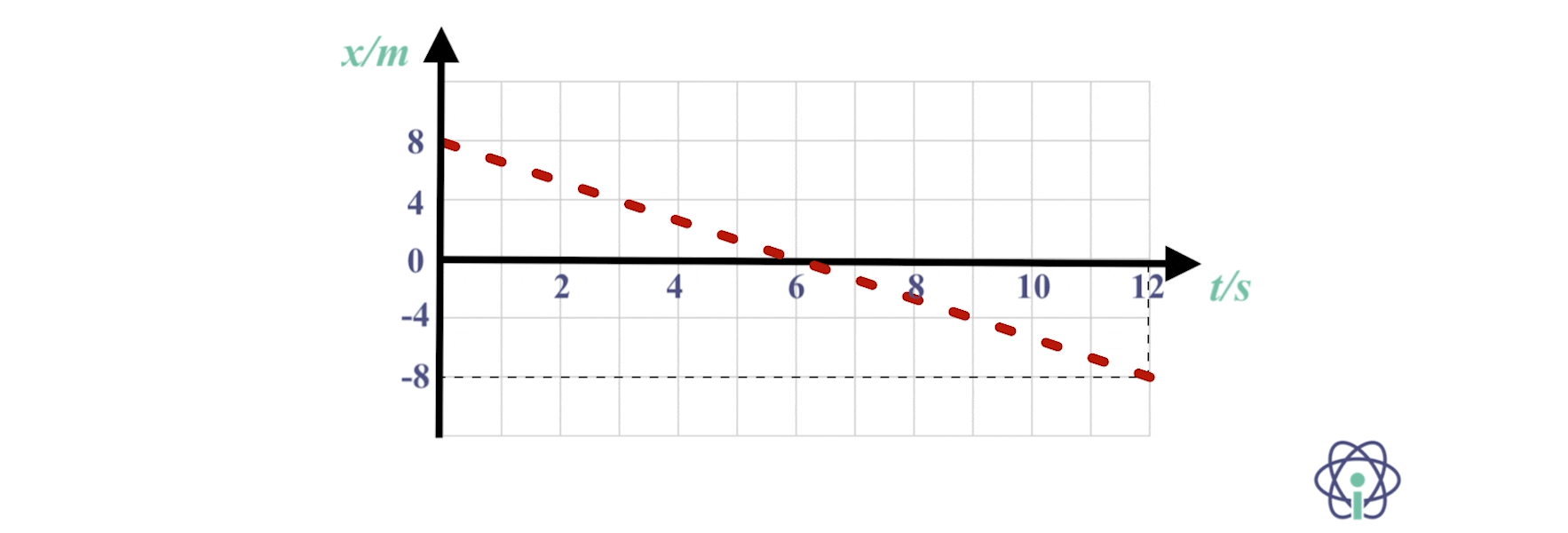
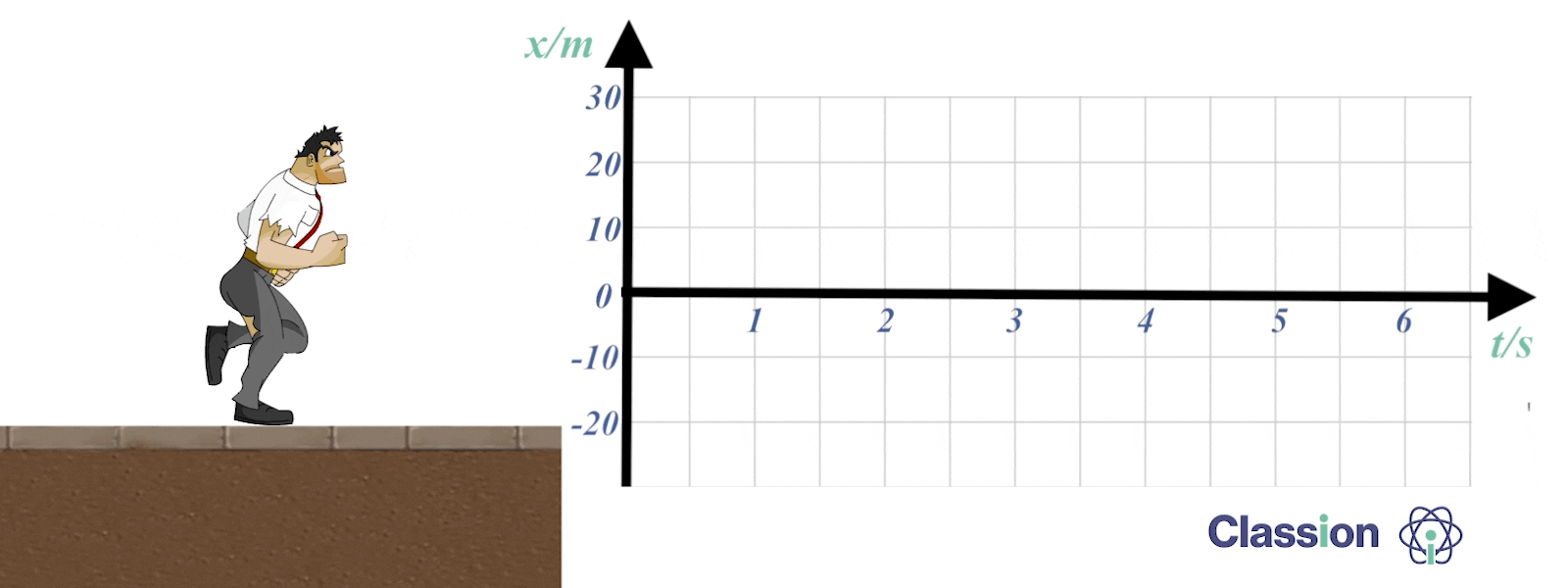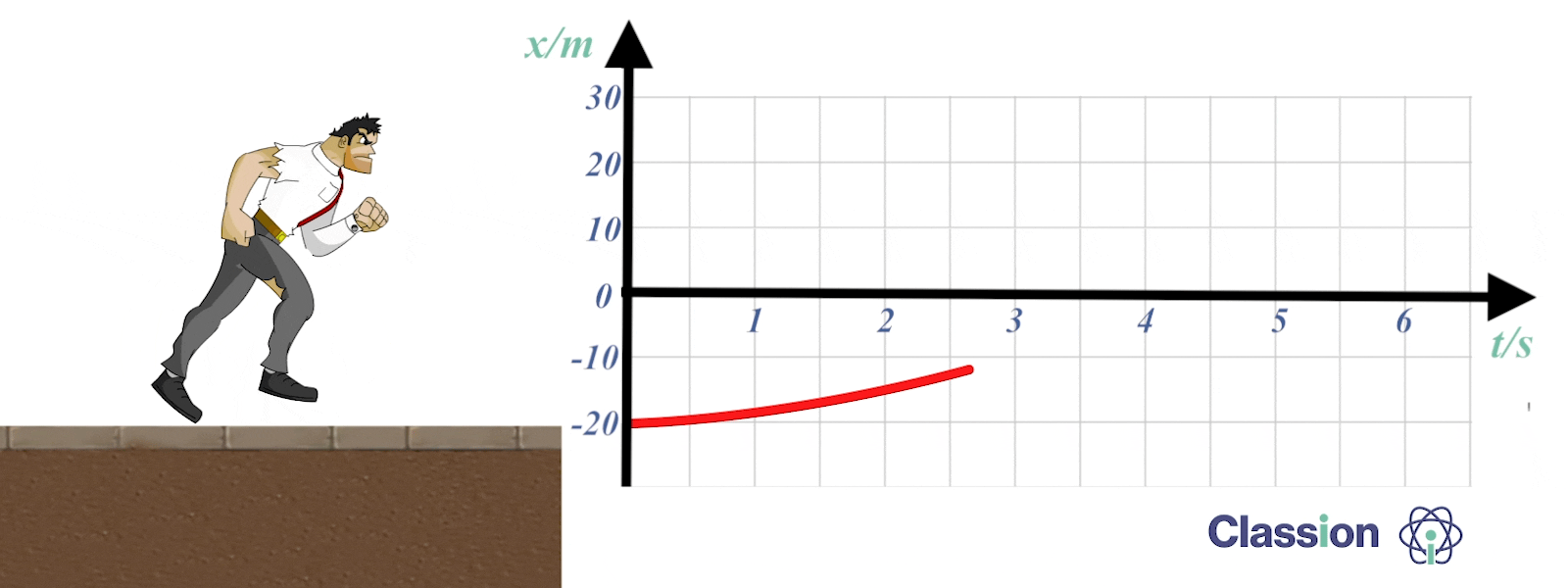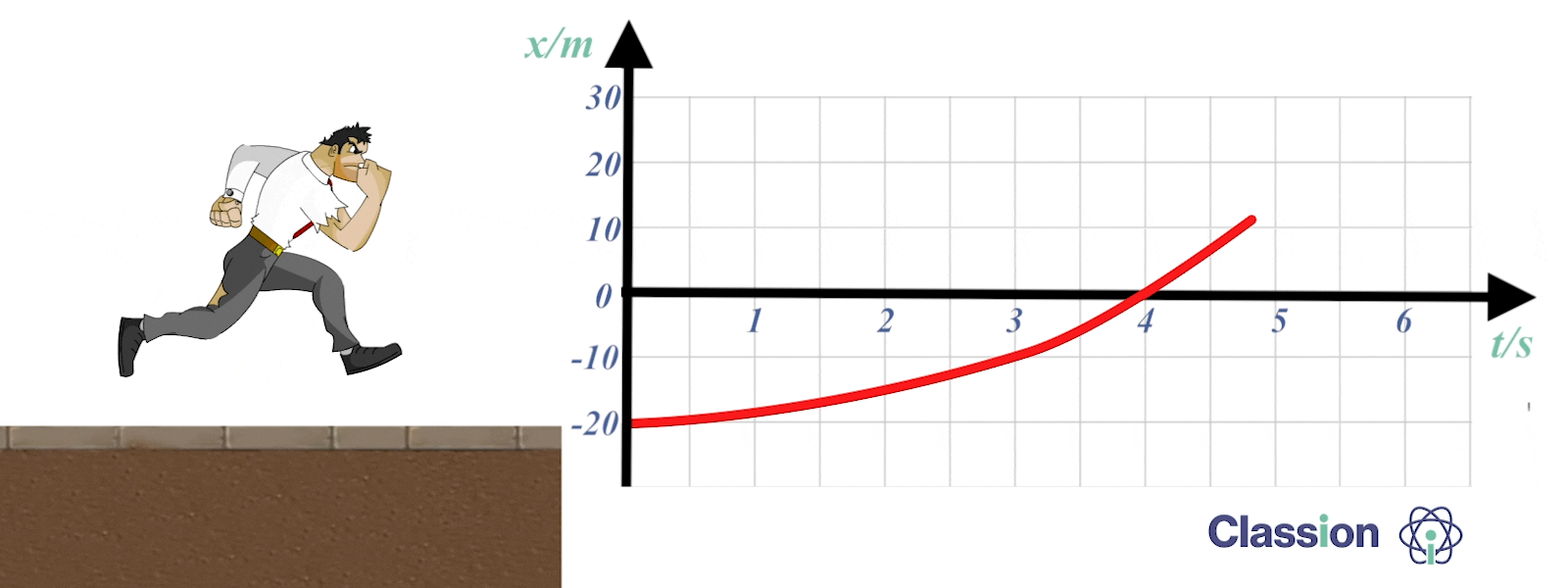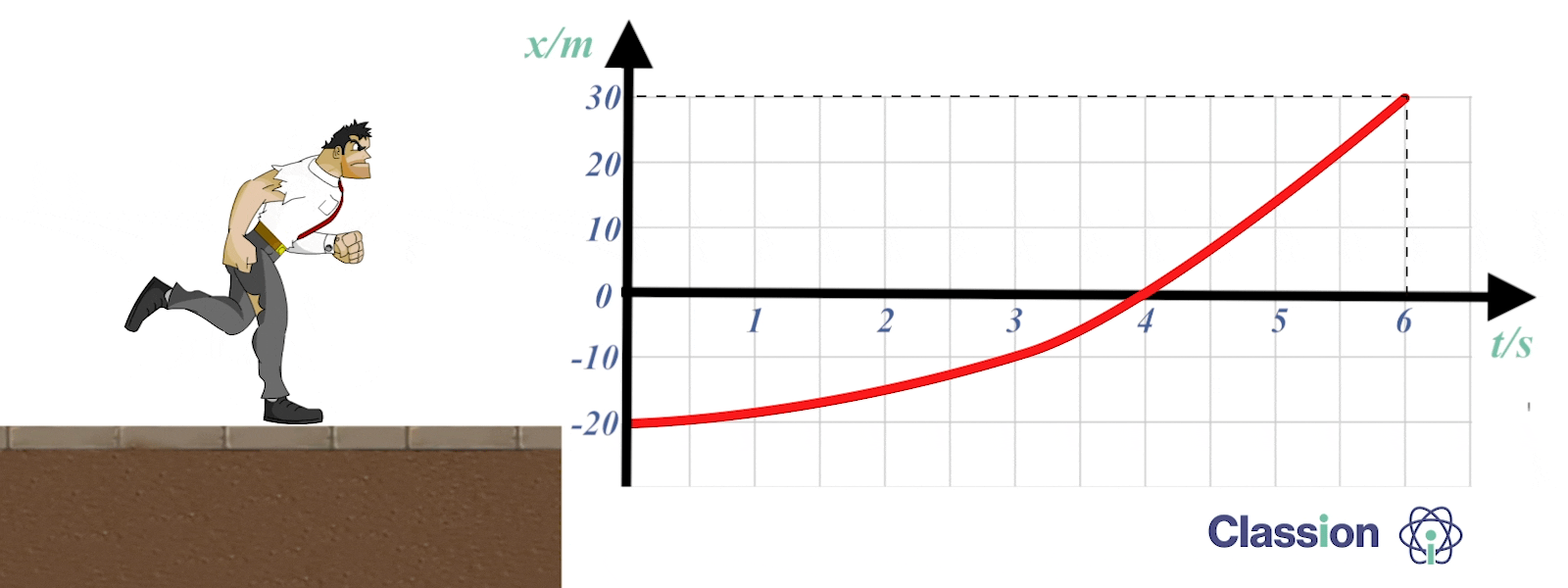
2. Gráfico posição em função do tempo representa o movimento do centro de massa de um carrinho.
2.1 Escreve a equação analítica das posições.
2.2 No instante t = 6,0 s, a componente escalar da velocidade do centro de massa do carrinho é
(A) 0,0 m s-1
(B) – 1,33 m s-1
(C) 1,33 m s-1
(D) – 2,67 m s-1
3. O Mario move um carro numa estrada retilínea coincidente com o referencial unidimensional Ox, sendo a equação que traduz o seu movimento:
x = 4,0 – 18,0 t + 3,0 t2 (SI)
Admita que o carro pode ser representado pelo seu centro de massa (modelo da partícula material).
3.1 Determina a distância percorrida pelo carro 30,0 s após iniciar o movimento.
3.2 A equação v(t) que traduz o movimento é ………… e a componente escalar da velocidade aos 7 s é ………
(A) … v = 2,0 – 2,0 t (SI) … v = – 12,0 m s-1
(B) … v = – 18,0 + 6,0 t (SI) … v = 24,0 m s-1
(C) … v = – 2,0 + 2,0 t (SI) … v = 12,0 m s-1
(D) … v = 18,0 – 6,0 t (SI) … v = – 24,0 m s-1
3.1 O carro inicia o movimento na posição 4,0 m.
⇒ A posição aos 30 s é
- x = 4,0 – 18,0 t + 3,0 t2 ⇔ x = 4,0 – 18,0 x 30,0 + 3,0 x 30,02 ⇔ x = 2164 m
⇒ O carro inverte o sentido aos 3 s na posição – 23 m, logo a distância percorrida será:
- d = | x3 – x0 | + | x30 – x3 | = | -23 – 4,0 | + | 2164 – ( -23) | = 2214 m
3.2
- Opção (B)
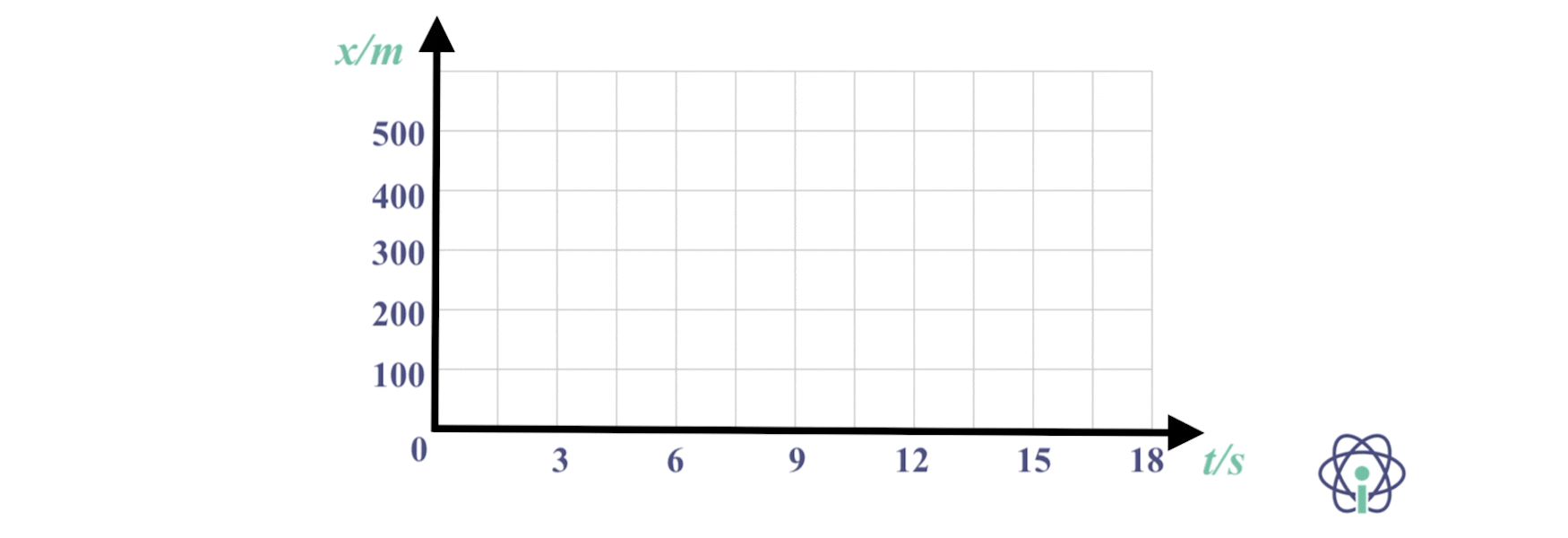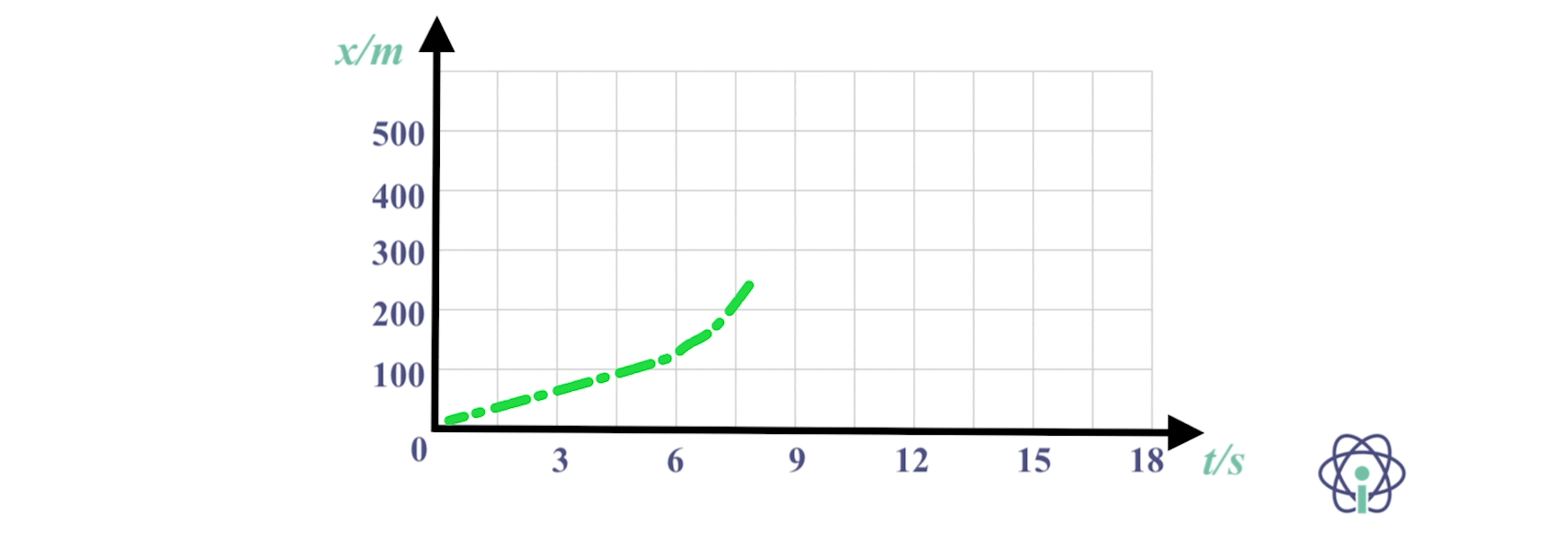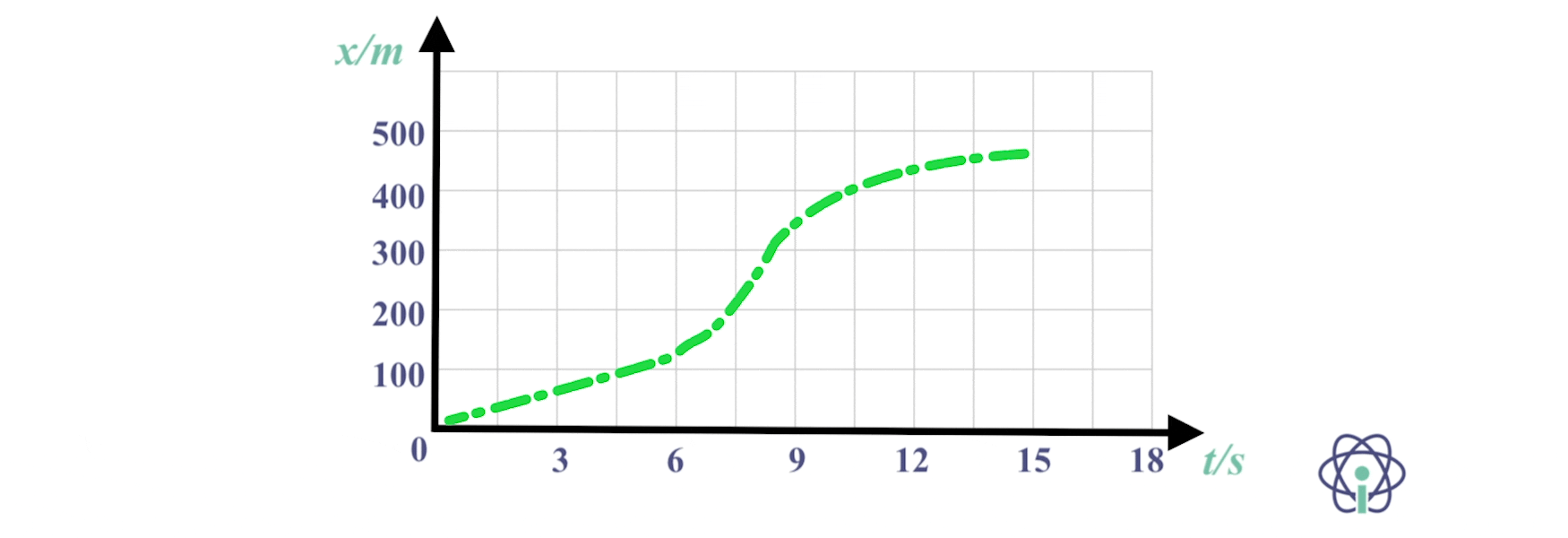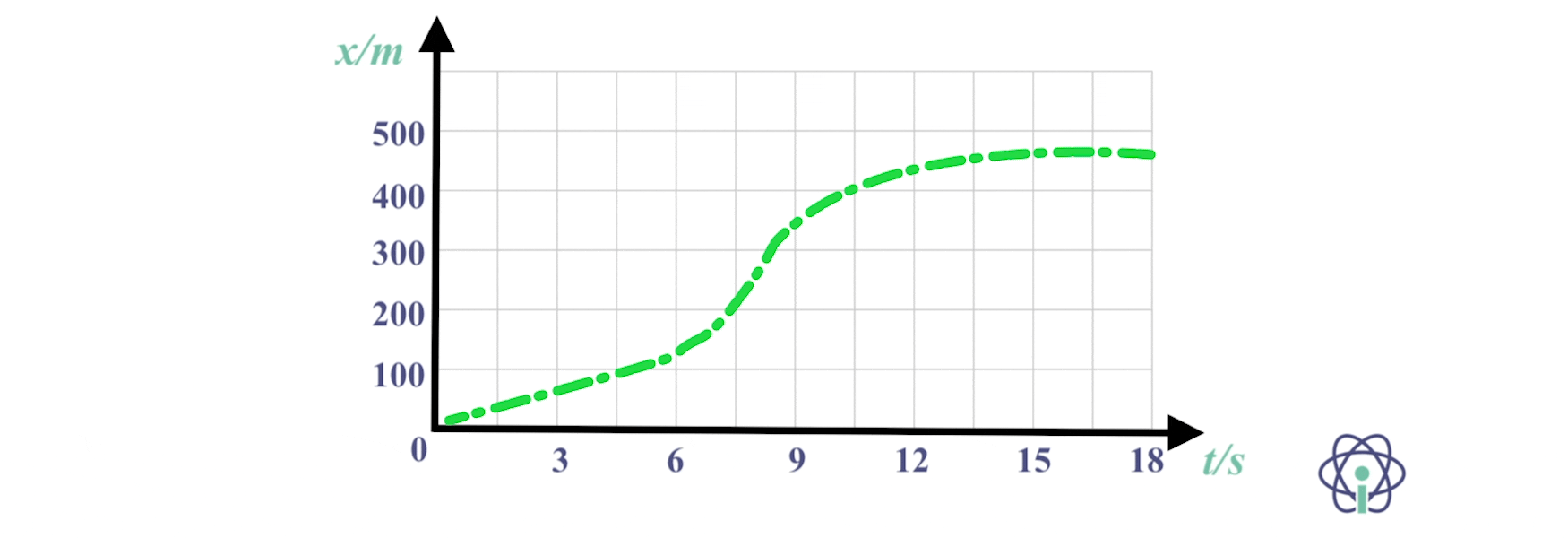
4. O João tem um movimento retilíneo e horizontal, sujeito a uma força cuja resultante e constante de módulo 160 N.
Considera a massa de 80 kg, no gráfico está caraterizada a posição em função do tempo.
4.1 Caracteriza o movimento do João no intervalo de tempo considerado.
4.2 Calcula o módulo da velocidade do João no início da contagem dos tempos.
4.3 Determina o módulo da velocidade do João no instante em que cumpriu 30,0 m de deslocamento.
4.1 Movimento retilíneo uniformemente acelerado.
4.2 Na posição t = 6,0 s, o João encontrava-se na posição x = 30 m;
⇒ Fr = ma ⇔ 160 = 80 x a ⇔ a = 2 m s-2
⇒ x = 30 = – 20 + v0 x 6,0 + 6,02 ⇔ v0 = 2,33 m s-1
4.3 No instante t = 6,0 s
⇒ v = 2,33 + 2,0 x 6,0 = 14,3 m s-1
5. Considera uma ambulância que se move, com aceleração constante, segundo uma trajetória retilínea, coincidente com o eixo Ox de um referencial unidimensional.
Admite que a componente escalar, segundo o eixo Ox, da posição, x, varia com o tempo, t, de acordo com a equação:
x(t) = 400 – 51 t + 3 t2 (SI)
5.1 Determina o instante para o qual a ambulância inverte o sentido do seu movimento;
5.2 Determina a posição em que se encontra a ambulância quando inverte o sentido do movimento.
5.3 Calcula a distância percorrida pela ambulância nos primeiros 5 s de movimento.
5.1 A ambulância inverte o seu movimento no instante em que a sua velocidade se anula:
- 0 = -51 + 6 t ⇔ t = 8,5 s
5.2
⇒ x = 400 – 51 x 8,5 + 3 x 8,52 = 183,2 m
5.3
⇒ d = |Δx| = | x6 – x0| = | 220 – 400| = |-180| = 180 m
6. O Alberto e a Rita num simulacro de incêndio, deslocam-se ao longo do tempo segundo uma trajetória retilínea com aceleração constante, segundo o eixo Ox.
O seu movimento é descrito de acordo com as seguintes equações:
- xAlberto = 4t2 (SI)
- xRita = 80 + 4t (SI)
Seleciona a opção correta.
(A) O Alberto e o Rita movem-se com a mesma aceleração.
(B) O movimento do Alberto é uniforme e o movimento do Rita é acelerado.
(C) A aceleração do Alberto é 8 m s-2 e a da Rita é nula.
(D) Entre os instantes t = 0 s e t = 2 s, o Alberto e a Rita percorrem a mesma distância.
- Opção (C)
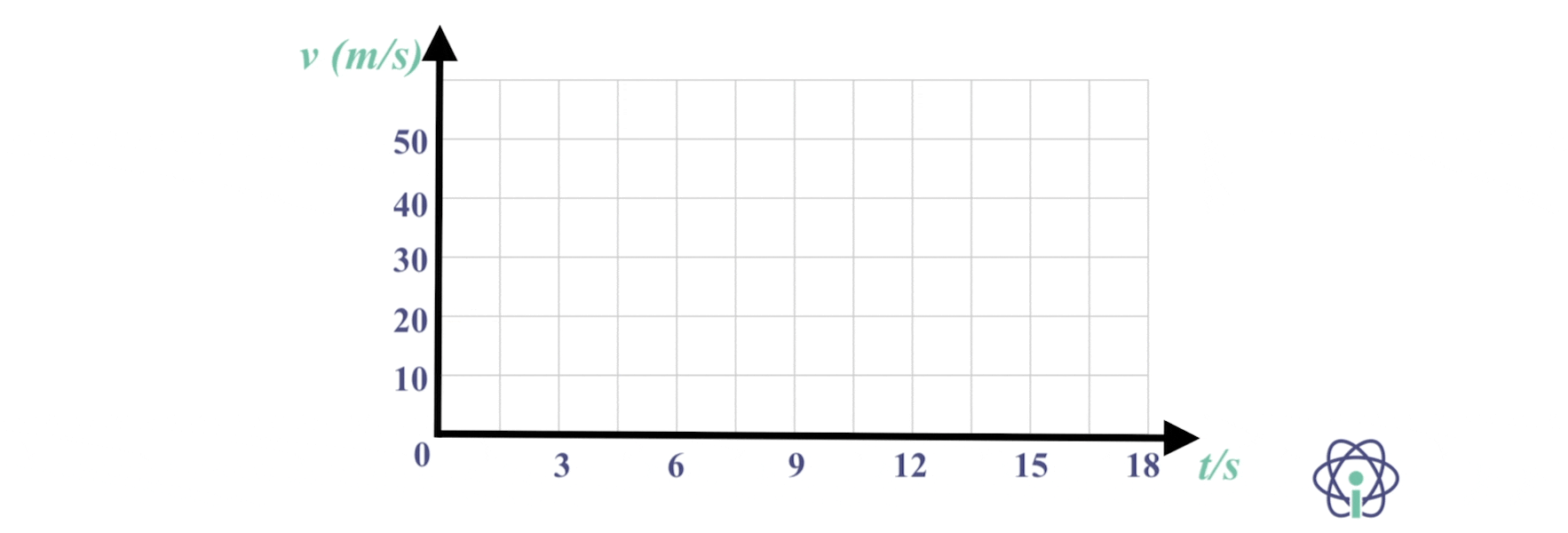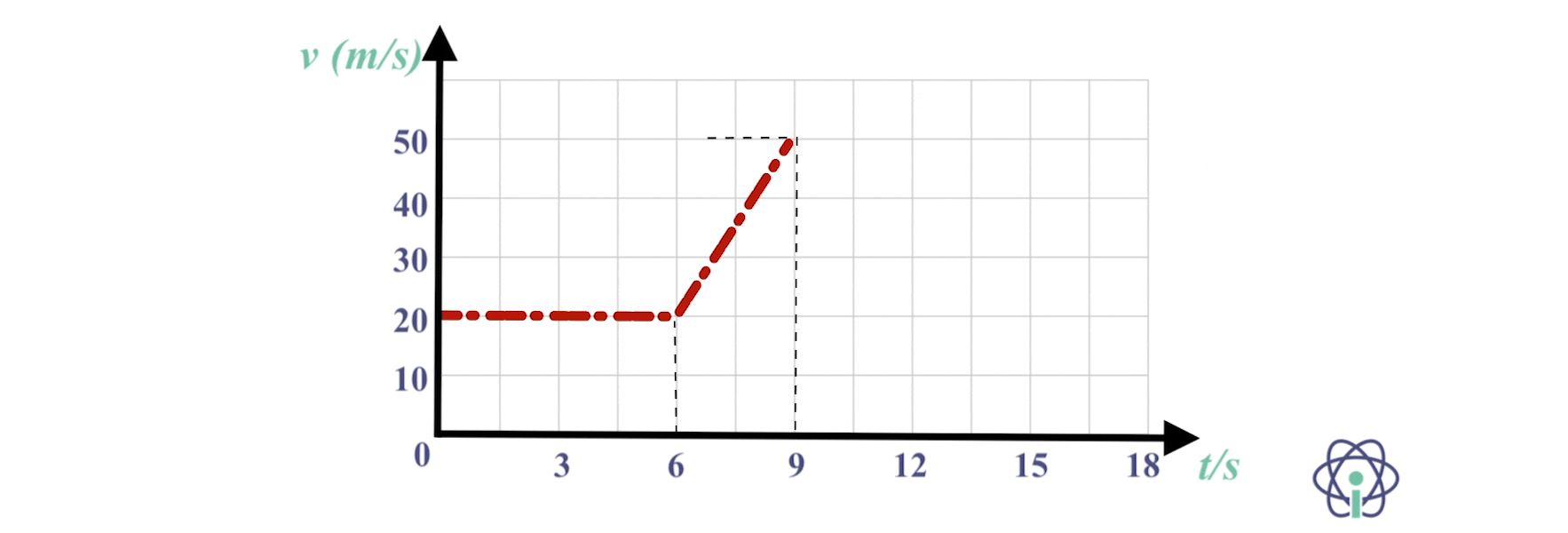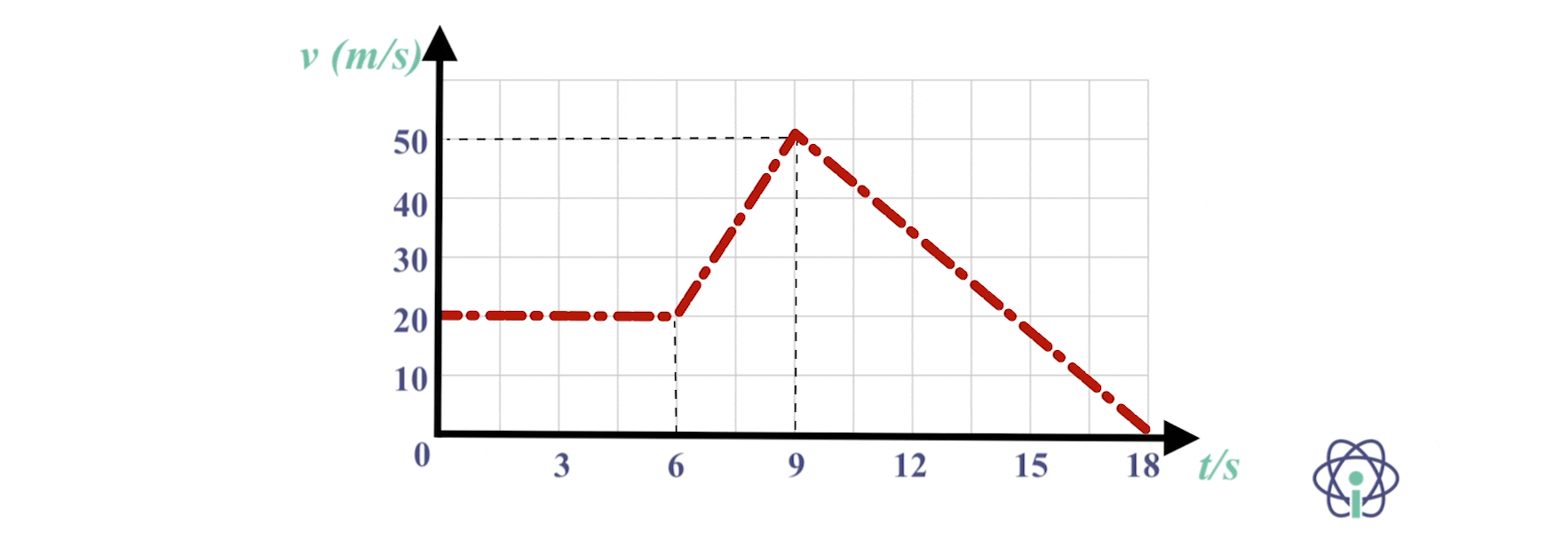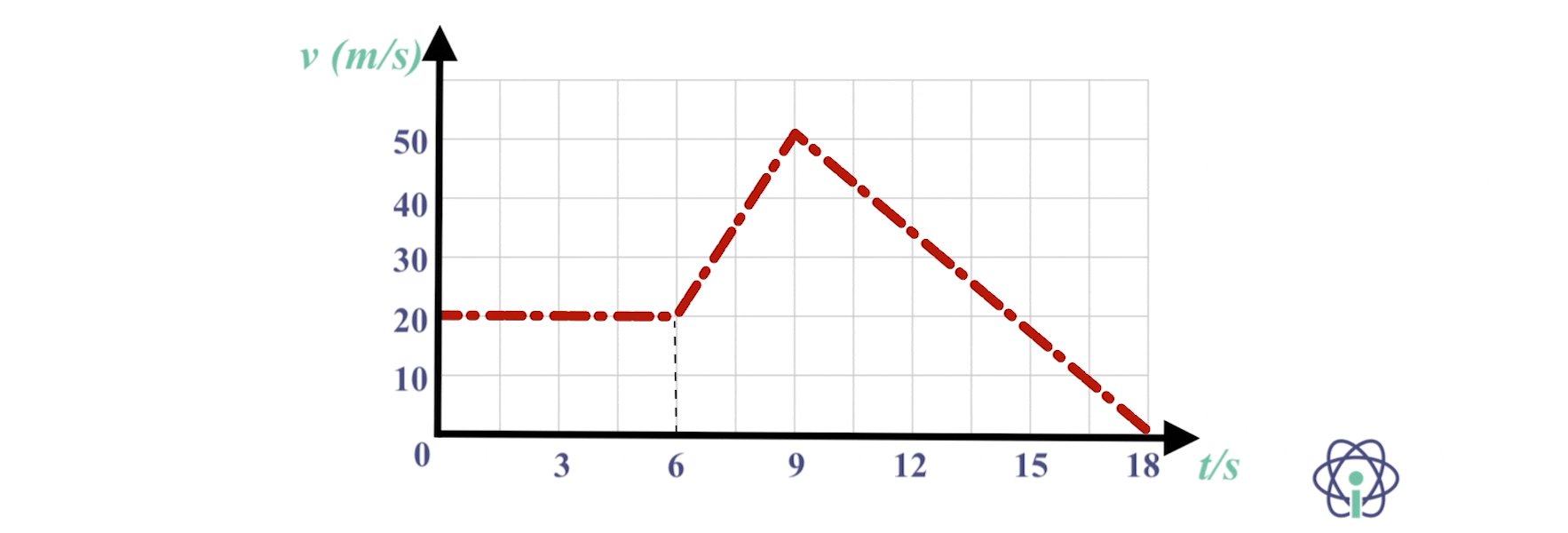
7*. O gráfico velocidade-tempo da figura diz respeito ao movimento retilíneo de uma carro, segundo a direção do eixo dos xx.
No instante inicial, t = 0 s, o carro encontra-se na posição x = 0 m.
7.1 Calcula, a partir do gráfico, a distância percorrida pelo corpo nos 18,0 s de movimento.
7.2 Calcula a componente escalar da aceleração nos instantes: t1 = 3,0 s, t2 = 7,0 se t3 = 14,0 s.
7.3 Esboça, o gráfico posição-tempo deste movimento.
7.1 A distância percorrida pelo carro, nos 18,0 s de movimento, calcula-se, a partir, pelas áreas.
Assim:
7.2 No instante t1 = 3,0 s, é a = 0 m s-2 , pois v = constante.
⇒ No instante t2 = 7,0 s, a componente escalar da aceleração é igual ao declive do segmento de reta no intervalo de tempo [6 ; 9] s
⇒ No instante t3 = 14,0 s, a componente escalar da aceleração é igual ao declive do segmento de reta no intervalo de tempo [9 ; 18] s
7.3
⇒ No intervalo de tempo [0 ; 6,0] s, o movimento é retilíneo uniforme, no sentido positivo do eixo dos xx, com x0 = 0 m, v = 20 m s-1 e x1 = 120 m
⇒ No intervalo de tempo [6,0 ; 9,0] s, o movimento é retilíneo uniformemente acelerado, no sentido positivo do eixo dos xx, com x1 = 120 m (posição final do movimento no intervalo de tempo [0; 6,0] s) e x2 = 120 + 225 = 345 m
⇒ No intervalo de tempo [9,0 ; 18] s, o movimento é retilíneo uniformemente retardado, no sentido positivo do eixo dos xx, com x2 = 345 m, e x3 = 450 m
8. Considera uma cama de 300 kg, partindo do repouso, foi acelerada até atingir a velocidade de módulo 15,0 m s-1 , ficando sujeito a uma resultante das forças constante de intensidade 1,80 x 103 N.
Considerando desprezável a resistência do ar e a força de atrito, determina a distância percorrida pela cama:
8.1 recorrendo exclusivamente às Leis de Newton e às equações do movimento.
8.2 recorrendo a considerações energéticas.
9. O Bernardo de 68 kg depois de uma festa esta sentado num bloco sobre uma superfície gelada, quando passaram uns amigos de hovercraft com uma massa total de 200 kg, atiram uma corda de 30 m e começaram a puxa-lo, aplicando uma força horizontal, de intensidade 150 N.
9.1 Calcula o módulo da aceleração do Bernardo e o módulo da aceleração do hovercraft.
9.2 Determina a que distância da posição inicial do Bernardo quando ele saltou para dentro do hovercraft.
9.1 Desprezando o atrito (porque superfície era gelada), a resultante das forças aplicadas sobre o Bernardo foi a força com que os amigos o puxaram.
⇒ Aplicando a 2ª lei de Newton, determina-se o módulo da aceleração do Bernardo:
A resultante das forças aplicadas sobre o hovercraft foi a força que o Bernardo aplicou nele através da corda.
⇒ O módulo da sua aceleração foi:
9.2 Primeiro deve-se escrever a equação das posições de cada um dos corpos.
⇒ Supondo que o sentido positivo do referencial é o sentido do movimento do Bernardo e que a origem do referencial é a sua posição inicial:
a aceleração do Bernardo tem sentido contrário à do hovercraft
⇒ Para determinar a posição em que os dois corpos se encontram começa-se por igualar as equações anteriores:
⇒ Substituindo este valor na equação das posições do Bernardo:
- O Bernardo e o hovercraft ficaram juntos a 22,4 m da posição inicial do Bernardo.
10. O Carlos foi correr e escorregou para dentro do caixote, o conjunto Carlos + caixote tem uma massa 700 kg, começou a deslocar-se ao longo de uma estrada retilínea partindo da posição inicial 20 m, sendo a equação do movimento v(t) traduzida por:
10.1 Determina a posição do conjunto no instante t = 4,0 s.
10.2 Qual o instante em que o conjunto inverte o sentido do movimento.
10.3 Determina a componente escalar do deslocamento e a distância percorrida pelo conjunto no instante t = 7,0 s.
10.4 Recorrendo às potencialidades gráficas da calculadora, determina o instante em que o conjunto passa pela origem das posições. Explicita o teu raciocínio.
10.1
⇒ y (4,0) = 20 + 30t – 3,0 t2 = 20 + 30 x 4,0 – 3,0 x 4,02 = 92 m
10.2
⇒ v = 30 – 6,0 t ⇔ 0 = 30 – 6,0 t ⇔ t = 5,0 s
10.3
⇒ Δx = xf – xi = 83 – 20 = 63 m
Como o conjunto inverte o sentido aos 5,0 s, a distância percorrida será superior à componente escalar do deslocamento e dependerá da posição ocupada nesse instante.
- y (5,0) = 20 + 30t – 3,0 t2 = 20 + 30 x 5,0 – 3,0 x 5,02 = 95 m
- y (7,0) = 20 + 30t – 3,0 t2 = 20 + 30 x 7,0 – 3,0 x 7,02 = 83 m
⇒ d = | x5,0 – x0,0 | + | x7,0 – x5,0 | = |95 – 20| + |95 – 83| = 87 m
10.4
⇒ O ponto obtido possui as coordenadas (10,6 ; 0,0), logo o conjunto passa pela origem das posições no instante 10,6 s
11. O Francisco estava na casa da árvore de altura 14 m, quando vê a frente de um camião a entrar na sua rua a uma distância de 18,0 m.
Nesse instante deixa cair um balde, e esperou que caísse em cima do camião.
O camião com 26 m de comprimento e 3,8 m de altura, movimentou-se com velocidade constante de módulo 18 m s-1, à medida que se foi aproximando da casa de onde caiu o balde. Verifica se o balde caiu em cima do camião.
- Camião:
⇒ A frente demorou 1,0 s a atingir o ponto por debaixo da casa.
x = x0 + v0t ⇔ 18,0 = 18,0 t ⇔ t = 1,0 s
⇒ Demorou 1,44 s a passar debaixo da casa.
x = x0 + v0t ⇔ 26,0 = 18,0 t ⇔ t = 1,44 s
- O balde:
⇒ O balde demorou s a atingir s a posição 3,8 m que coincide com a altura do camião.
- y = y0 + v0t + ½at2 ⇔ 3,8 = 14,0 – 5 t2 ⇔ t = 1,43 s
⇒ Podemos concluir que o balde caiu em cima do camião.
12. Se um carro que se move com velocidade constante, podemos afirmar que …
(A) percorre distâncias iguais no mesmo intervalo de tempo, não sendo nula a resultante das forças.
(B) tem uma velocidade média que é, em qualquer intervalo de tempo, igual à velocidade em qualquer instante.
(C) descreve uma trajetória retilínea com inversão de sentido.
(D) pode descrever uma trajetória curvilínea desde que a aceleração seja constante.
- Opção (B)
⇒ Para o movimento retilíneo e uniforme, a velocidade média em qualquer intervalo de tempo é igual à velocidade instantânea pois esta é constante.
13. Uma partícula com uma velocidade igual a 10% da velocidade da luz no vazio (3,0 x 108 m s-1), move-se retilíneamente.
Entrou num campo elétrico, passa a movimentar-se com aceleração constante de módulo 1,0 x 1012 m s-2 e contrária à sua velocidade.
Assinala a equação que descreve a componente escalar da velocidade da partícula dentro do campo elétrico.
(A) v = 3,0 x 107 – 1,0 x 1012 t (SI)
(B) v = 3,0 x 107 – 0,50 x 1012 t (SI)
(C) v = 3,0 x 108 + 1,0 x 1012 t (SI)
(D) v = 3,0 x 108 – 0,50 x 1012 t (SI)
- Opção (A)
14. O Gabriel desloca uma máquina de lavar ao longo de um trajetória retilínea, sendo a equação do movimento x(t) dada por:
x = – 20,0 + 2,0 t (SI)
Admite que o Gabriel pode ser representado pelo seu centro de massa (modelo da partícula material) e considera um referencial unidimensional Ox, coincidente com a direção e sentido do movimento.
14.1 A Gabriel parte da posição …….. e passa pela origem das posições aos …………. com componente escalar de velocidade ……….. .
(A) … – 20,0 m … 0,0 s .. . 0 m s-1
(B) … – 20,0 m … 10,0 s … 2,0 m s-1
(C) … 10,0 m … 10,0 s … – 20,0 m s-1
(D) … 10,0 m .. . 0,0 s … 0 m s-1
14.2 Uma vez iniciado o movimento, determina ao fim de quanto tempo o Gabriel percorre 300 m.
14.1 Opção (B)
14.2 O Gabriel inicia o movimento na posição – 20,0 m e desloca-se no sentido positivo d trajectória, sem inversão de sentido. Logo, atinge uma distância percorrida de 300 m quando se encontra na 280 m.
- x = – 20,0 + 2,0 t ⇔ 280 = -20,0 + 2,0 t ⇔ t = 150 s
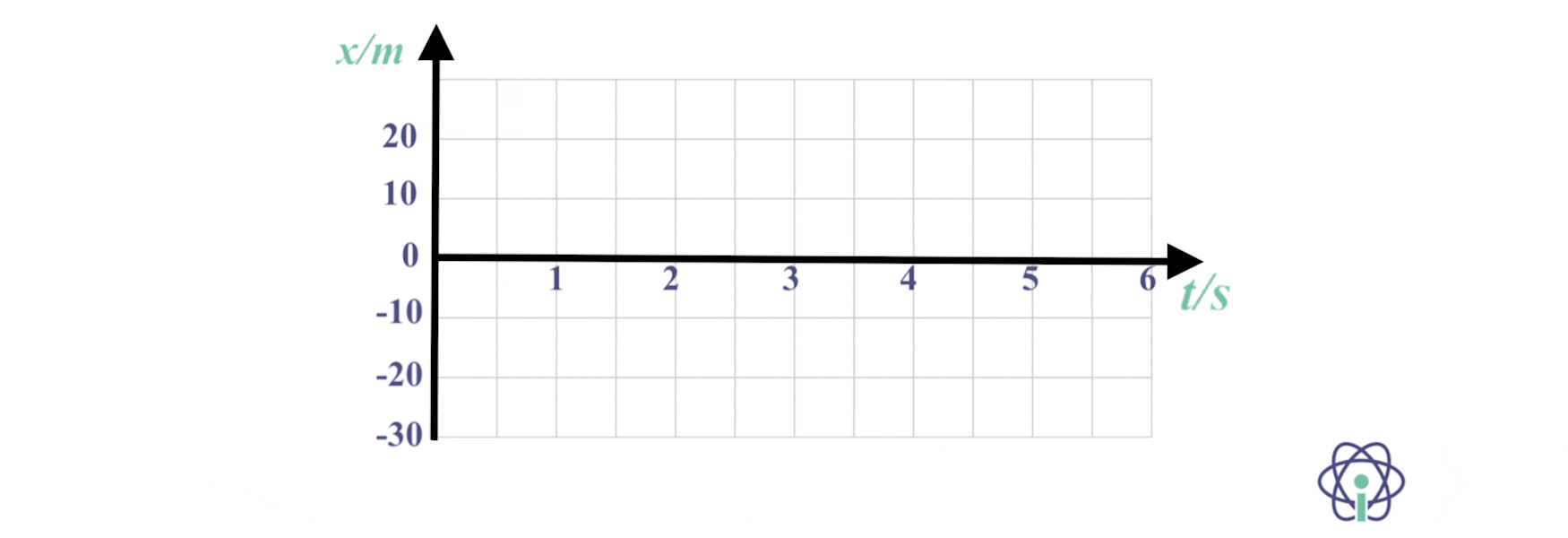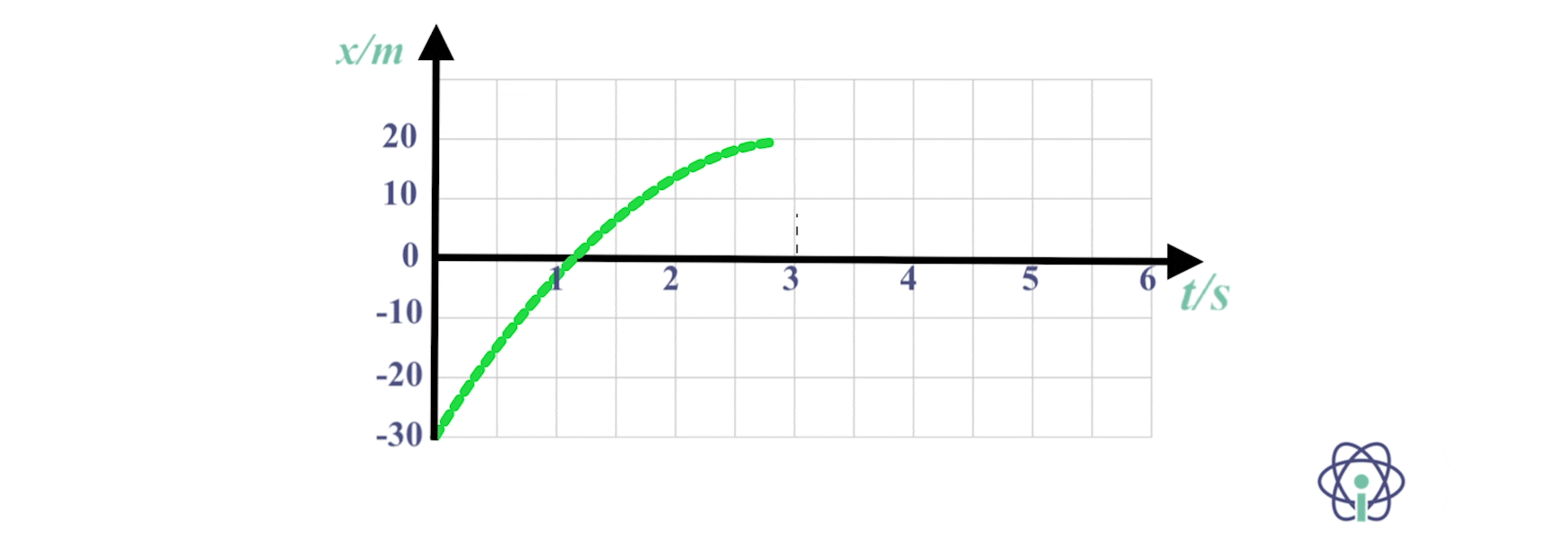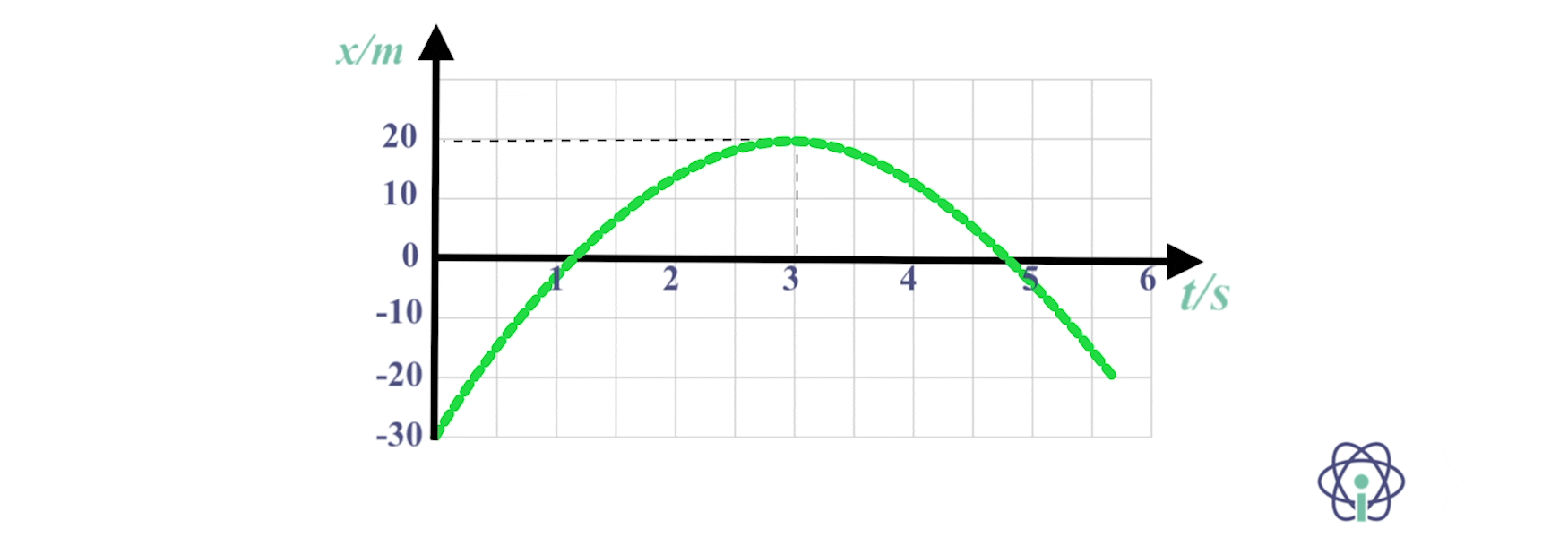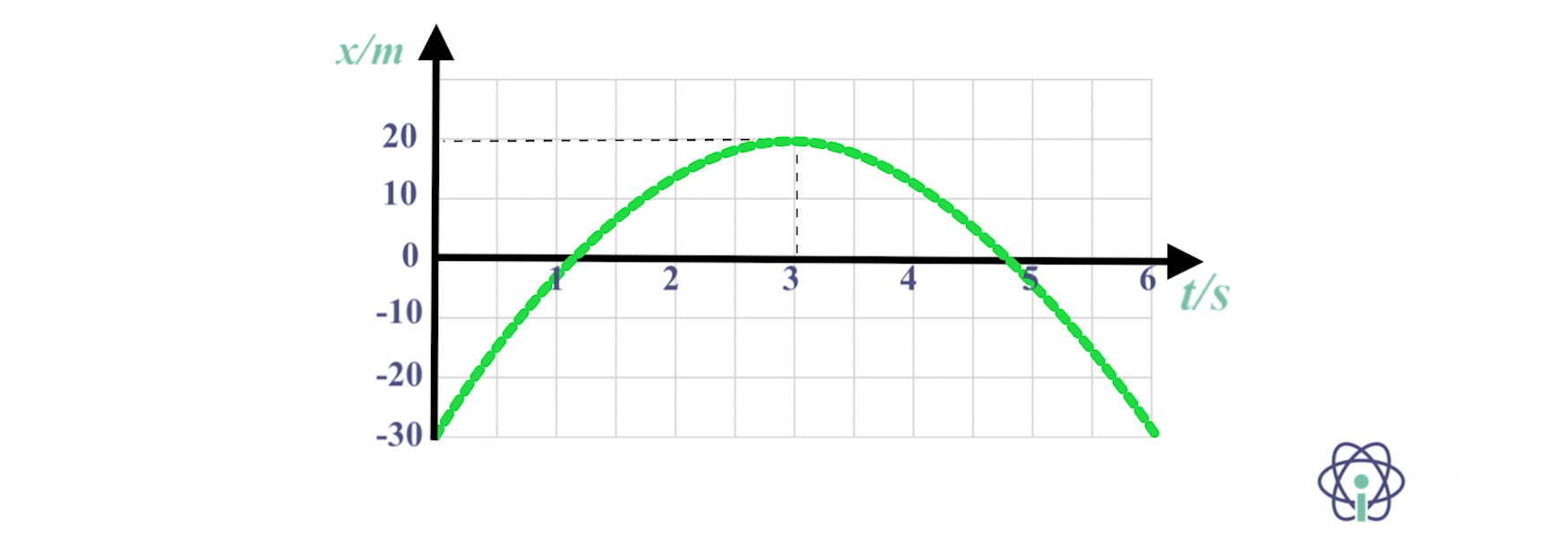
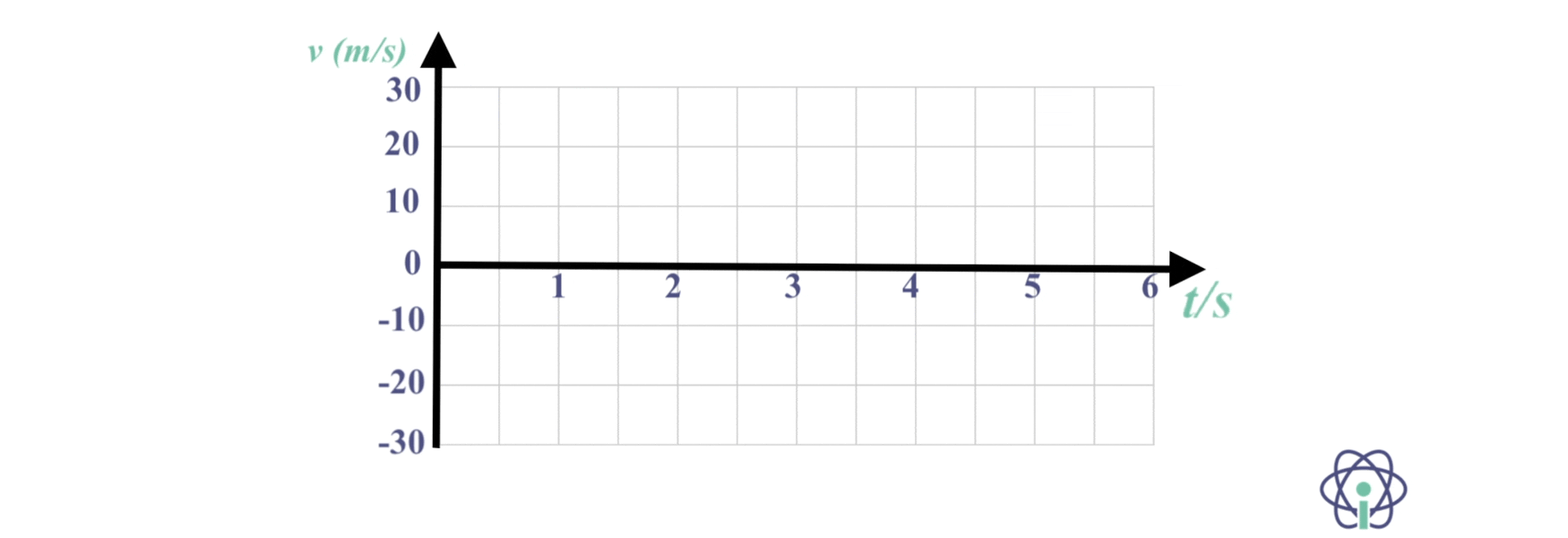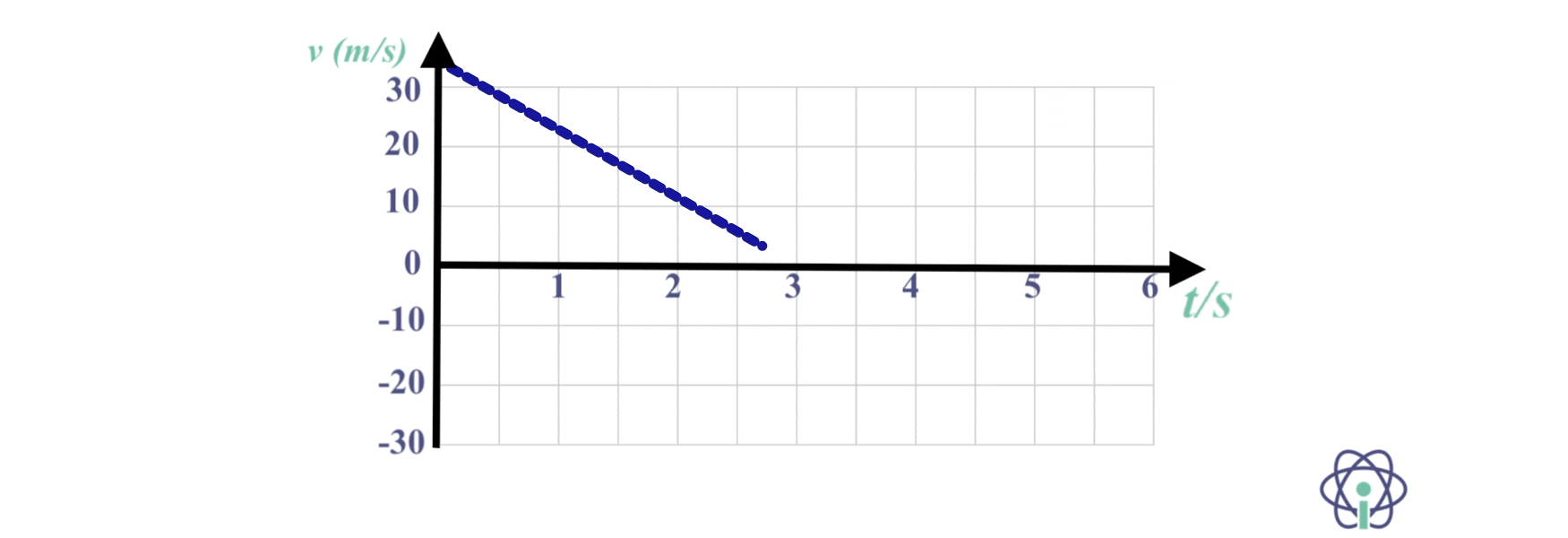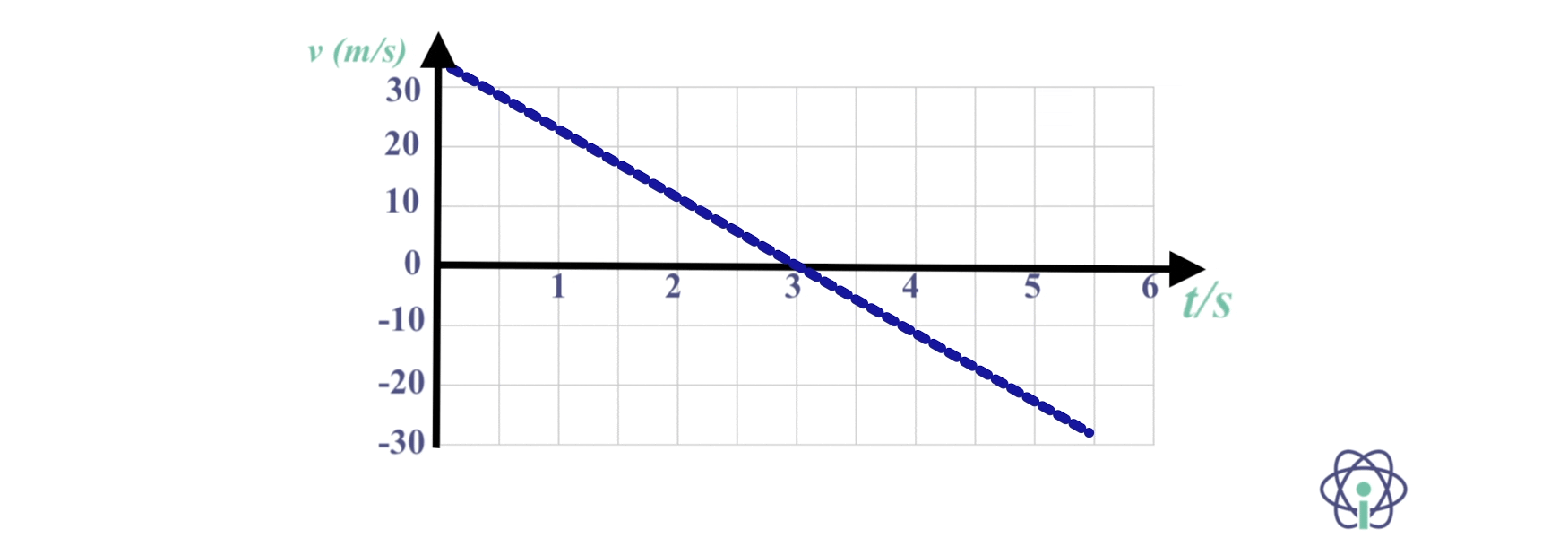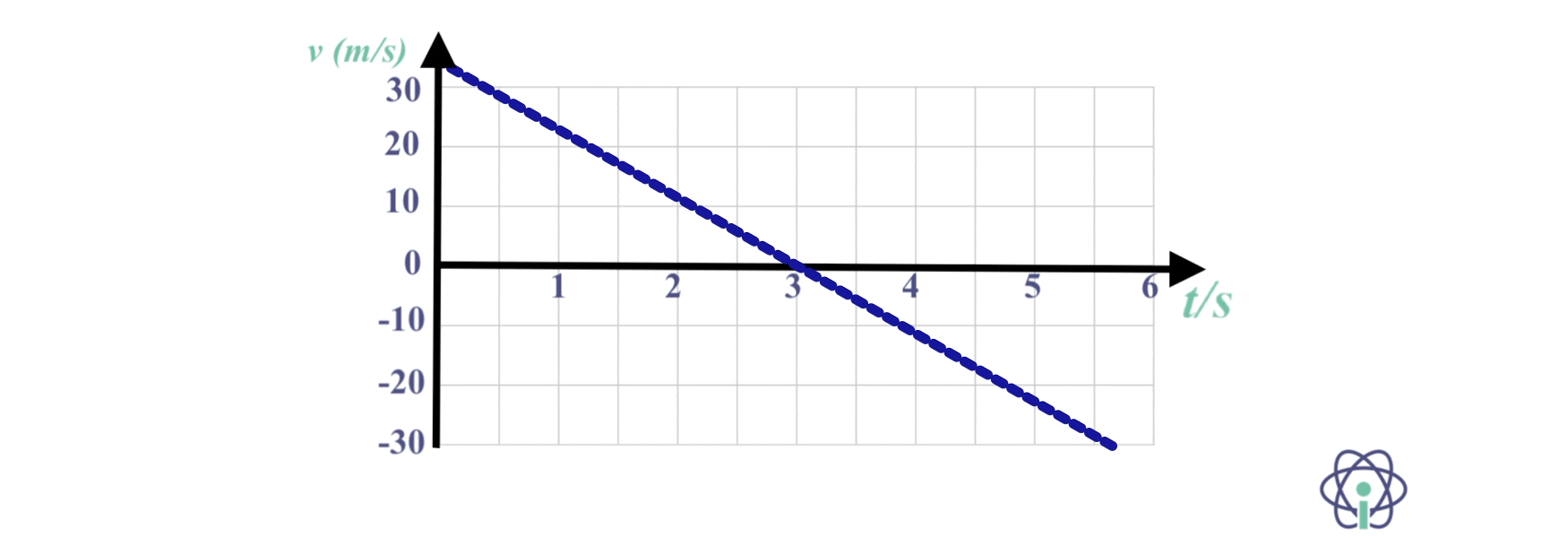
15. O gráfico da figura indica as posições de um corpo com movimento retilíneo, em função do tempo.
15.1 Determina a componente escalar da aceleração e da velocidade inicial, usando as equações do movimento.
15.2 Traça o gráfico v = f(t) correspondente a este movimento.
15.1 A velocidade é nula no instante t = 3,0 s (reta tangente ao gráfico nesse instante tem declive nulo).
⇒ Resolvendo em simultâneo as equações do movimento para esse instante:
- x = 20 = -30 + v0 x 3,0 + 0,5 a x 3,02
- v = 0 = v0 + a x 3,0
⇒ 50 = 3,0 x ( – 3,0 a) + 4,5 a ⇔ 50 = -4,5 a ⇔ a = – 11,1 m s-2
⇒ v0 = – a x 3,0 = 33,3 m s-1
As leis do movimento são:
- x = – 30 + 33,3 t – 5,55 t2 (SI)
- v = 33,3 – 11,1 t (SI)
15.2