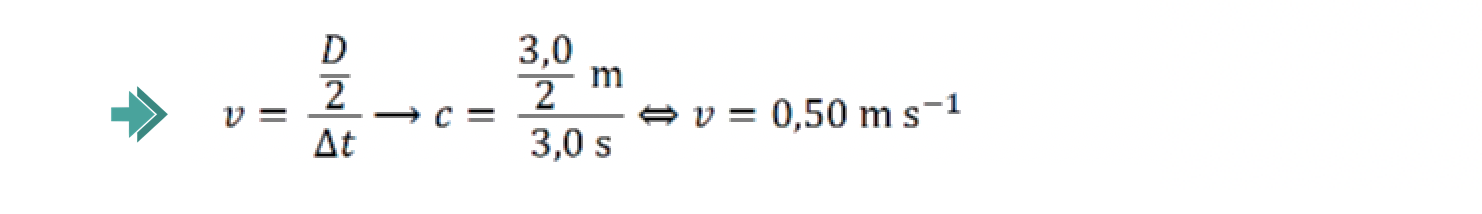Ficha nº3 : Exames e TI (2018 – 202*)
Voltar a: 11ºAno – Física
Ficha nº3
Exercícios de exames e testes intermédios (2018 – 202*)
11ºano – Física – Domínio 2 – Subdomínio 1 (Sinais e ondas)
1. (2018 – 1ªF) Quando um sinal sonoro se propaga no ar, há variações de pressão em cada ponto.
1.1. Na Figura 3, está representada, num certo instante, uma determinada região do espaço em que se propaga, da esquerda para a direita, um sinal sonoro de período T .
As zonas mais escuras correspondem a zonas de compressão do ar, e as zonas mais claras correspondem a zonas de rarefação.
Na figura, encontra-se ainda representada, pela linha a tracejado, P, uma certa camada de ar naquela região do espaço.
Qual das figuras seguintes pode representar, um período e meio depois, a mesma região do espaço e a mesma camada de ar?
- Opção (A)
⇒ Nas ondas sonoras, as camadas de ar oscilam em torno das suas posições de equilíbrio, originando zonas de compressão e zonas de rarefação do ar.
⇒ Ocorre transferência de energia de umas camadas para as outras, mas não há transporte de matéria, ou seja, cada camada de ar permanece na sua posição média no espaço.
⇒ A Figura 3 mostra que a camada de ar identificada pela linha P corresponde a uma zona de compre são do ar, situação esta que volta a verificar-se após qualquer número inteiro de períodos, T, 2 T, etc.
⇒ Entre duas situações consecutivas de compressão, a camada de ar passa por uma situação de rarefação.
⇒ Quando tiver decorrido um período e meio, a camada de ar P já terá passado por uma nova situação de compressão e estará numa situação de rarefação.
- Opção (A) ……………. 6 pontos
1.2. Um sinal sonoro foi convertido num sinal elétrico e analisado num osciloscópio, cuja base de tempo estava regulada para 0,5 ms por divisão.
Na Figura 4, está representada a imagem obtida no ecrã do osciloscópio.
Verificou-se experimentalmente que, em determinadas condições, um pulso do mesmo som demorava 5,78 x 10-2 s a percorrer uma distância de 20,0 m no ar.
Determine o comprimento de onda do som no ar, naquelas condições.
Apresente todas as etapas de resolução.
- Etapas de resolução:
⇒ Determinação do período do sinal sonoro (T = 1,50 ms ) …….. 3 pontos
⇒ Determinação do módulo da velocidade de propagação do sinal no ar, nas condições em que decorreu a experiência (v = 346,0 m s-1) …….. 3 pontos
⇒ Cálculo do comprimento de onda do som no ar, nas condições em que decorreu a experiência (λ = 0,52 m) …….. 4 pontos
2. (2018 – EE) Os golfinhos dependem da emissão e da receção de sons para se orientarem, comunicarem entre si e caçarem.
2.1. As ondas sonoras são ondas mecânicas que, na água, são longitudinais.
Apresente, num texto estruturado e utilizando linguagem científica adequada, o significado da afirmação anterior.
⇒ A afirmação classifica as ondas sonoras que se propagam na água como sendo simultaneamente ondas mecânicas e ondas longitudinais.
⇒ A onda sonora é uma onda mecânica porque precisa de um meio material para se propagar, que neste caso é a água.
⇒ Uma onda sonora na água é a propagação de uma perturbação na pressão da água e, embora as partículas que constituem o meio não sejam transportadas com a onda, são as oscilações de cada uma dessas partículas que dão origem à variação de pressão e a transmitem às partículas vizinhas.
⇒ A onda sonora na água é uma onda longitudinal porque a onda se propaga na mesma direção da variação da propriedade física, que neste caso é a pressão.
⇒ Sendo uma onda mecânica e longitudinal, a direção de propagação da onda é igual à direção de oscilação das partículas do meio.
- Tópicos de resposta:
A) As ondas sonoras serem ondas mecânicas significa que a propagação de um sinal sonoro necessita de um meio material.
B) Na água, as ondas sonoras serem longitudinais significa que a direção de vibraçãodo meio coincide com a direção de propagação do sinal sonoro.
2.2. Um golfinho emite um som à superfície da água do mar que é detetado por dois sensores colocados à mesma distância do golfinho, um dentro de água e outro no ar.
O som demora 0,10 s a chegar ao sensor que se encontra dentro de água e demora mais 0,34 s a chegar ao sensor que se encontra no ar.
Qual é o quociente entre a velocidade de propagação do som na água do mar e a velocidade de propagação do som no ar, nas condições em que decorreu a experiência?
(A) 3,4
(B) 4,4
(C) 0,23
(D) 0,29
- Opção (B)
⇒ A velocidade de propagação de uma onda, v, é dada por
onde s é a distância percorrida pela onda no intervalo de tempo Δt. A velocidade depende do meio, o que corresponde, neste caso, a dizer que Vágua ≠ Var.
⇒ Consequentemente, a mesma distância s = ságua = sar é percorrida em intervalos de tempo diferentes nos dois meios:
- Opção (B) ……………. 6 pontos
2.3. O gráfico da Figura 4 representa, para um determinado local, a velocidade de propagação do som na água do mar em função da profundidade.
Fonte: w3.ualg.pt/~prelvas/OceanogFisica/Prop_som.pdf (consultado em março de 2018)
Considere um som puro que se propaga na água do mar, atravessando as três regiões consideradas.
A partir do gráfico, pode concluir-se que, à profundidade h1, _____ desse som atinge um valor _______.
(A) a frequência … mínimo
(B) a frequência … máximo
(C) o comprimento de onda … mínimo
(D) o comprimento de onda … máximo
- Opção (C)
⇒ Uma onda é caracterizada por dois parâmetros, o comprimento de onda, λ, e a frequência, f, cujo produto é a velocidade de propagação da onda: v = λ f .
⇒ A velocidade depende das características do meio cm que a onda se propaga, o que conduz, neste caso, a uma variação da velocidade com a profundidade da água do mar, h, descrita pela função v = v(h).
⇒ A frequência só depende da fonte geradora das ondas, pelo que permanece constante quando varia a profundidade h.
⇒ O comprimento de onda será dado por uma função λ = λ(h) com a mesma forma da função v(h).
⇒ De acordo com a Figura 4, a velocidade atinge um valor mínimo à profundidade h1, o comprimento de onda atinge também um valor mínimo a essa profundidade.
- Opção (C) ……………. 6 pontos
3. (2019 – 1ªF) Uma tina de ondas é um tanque de pequena profundidade que contém água e onde é possível, utilizando um gerador adequado, produzir ondas na superfície da água.
O gerador pode ser ajustado de modo a produzir ondas de frequências diferentes.
As imagens dessas ondas apresentam zonas mais claras, que correspondem a cristas , e zonas mais escuras, que correspondem a vales.
A Figura 1 apresenta uma imagem das ondas obtidas numa tina de ondas , numa determinada experiência.
Na figura, estão ainda representados dois pontos, A e B, à superfície da água.
3.1. Considere que o gerador de ondas está ajustado para 5,0 Hz e que a imagem é obtida num instante t.
Quanto tempo decorrerá, no mínimo , entre o instante t e um instante no qual o ponto A se encontre num vale?
(A) 0,15 s
(B) 0,20 s
(C) 0,050 s
(D) 0,10 s
- Opção (D)
⇒ Sendo a frequência f = 5,0 Hz, o período vem dado por T=1/f = 1/5,0 = 0,20 s.
⇒ Como o ponto A está assinalado numa zona clara, o que corresponde a uma crista, o tempo mínimo que terá de decorrer até que o ponto A se encontre num vale corresponderá a meio período, T/2 = 0,10 s.
- Opção (D) ……………. 7 pontos
3.2. Se a distância entre os pontos A e B for 15,6 cm, o comprimento de onda das ondas que se propagam na superfície da água será
(A) 1,30 cm
(B) 2,23 cm
(C) 2,60 cm
(D) 3, 12 cm
- Opção (C)
⇒ A distância entre A e B corresponde a 6 comprimentos de onda.
⇒ O comprimento de onda é, assim, dado por λ = 15,6/6 = 2,60 cm.
- Opção (C) ……………. 7 pontos
4. (2019 – 1ªF) Com o objetivo de determinar a velocidade de propagação das ondas produzidas na superfície da água contida numa tina, mediu-se o comprimento de onda, λ, dessas ondas para várias frequências, f.
Na tabela seguinte, estão registados os valores de f e de λ medidos e ainda os inversos desses valores.
Determine a velocidade de propagação das ondas, em cm s-1, nas condições em que decorreu a experiência, a partir da equação da reta de ajuste a um gráfico adequado.
Na sua resposta:
– identifique as variáveis independente e dependente a considerar nos eixos do gráfico;
– apresente a equação da reta de ajuste ao gráfico;
– obtenha o valor solicitado, com um número correto de algarismos significativos.
Apresente todas as etapas de resolução, explicitando todos os cálculos efetuados.
⇒ Sendo o módulo da velocidade de propagação de uma onda dado pela expressão: v = λ f , é possível determiná-lo, a partir de um conjunto de medições e fazendo um ajuste linear aos valores dessas medições.
⇒ Considerando que λ =v/f, o comprimento de onda será a variável dependente e 1/f a variável independente a considerar nos eixos do gráfico seguinte:
⇒ Nesta situação, obtém-se por regressão linear a seguinte equação da reta:
⇒ O declive da reta é o módulo da velocidade de propagação das ondas produzidas, v = 20 cm s-1.
⇒ O menor número de algarismos significativos dos dados é dois, consequentemente o resultado final não poderá ter um número de algarismos significativos superior a esse.
⇒ O valor da ordenada na origem pode ser considerado nulo dentro das incertezas das medidas, como seria de esperar atendendo à expressão v = λ f .
⇒ O módulo da velocidade de propagação pode ser obtido de modo idêntico, considerando a relação:
- em que a frequência será a variável independente e 1/λ a variável dependente a considerar nos eixos do gráfico.
⇒ Nesta opção, o módulo da velocidade será o inverso do declive obtido.
- Etapas de resolução:
⇒ Apresentação da equação da reta de ajuste
ou
⇒ Apresentação da equação da reta de ajuste (ver nota) …….. 5 pontos
⇒ Determinação da velocidade de propagação das ondas, com um número correto de algarismos significativos (v = 20 cm s-1) …….. 5 pontos
Nota ‒ A omissão da ordenada na origem não implica qualquer desvalorização
5. (2019 – EE) A Figura 1 representa um gerador de sinais ligado a um altifalante e um microfone ligado a um osciloscópio. O gerador de sinais produz um sinal elétrico que é convertido num sinal sonoro pelo altifalante.
Este sinal sonoro é detetado pelo microfone, que o converte num sinal elétrico que é visualizado no ecrã do osciloscópio.
Figura 1
A Figura 2 representa o sinal elétrico visualizado no ecrã do osciloscópio, quando a base de tempo do osciloscópio está regulada para 250 μs por divisão e o amplificador vertical está regulado para 5 mV por divisão.
Figura 2
5.1. O sinal visualizado no ecrã do osciloscópio tem um período de _____ e uma amplitude de _____.
(A) 1,1 ms … 14 mV
(B) 4,5 ms … 14 mV
(C) 1,1 ms … 28 mV
(D) 4,5 ms … 28 mV
- Opção (A)
⇒ O Período do sinal é igual ao intervalo de tempo que decorre entre dois instantes na mesma fase, o intervalo de tempo entre dois máximos consecutivos da onda observada no osciloscópio.
⇒ A amplitude da onda é igual ao módulo do valor máximo (ou mínimo) da onda.
Assim:
⇒ A = 2,8 x 5 mV = 14 mV
⇒ T = 4,4 x 250 μs = 1,1 x 103 μs = 1,1 x 103 x 10-3 ms = 1,1 ms
- Opção (A) ……………. 7 pontos
5.2. O sinal sonoro produzido pelo altifalante e o sinal sonoro detetado pelo microfone terão frequências _____ e intensidades _____ .
(A) diferentes … iguais
(B) diferentes … diferentes
(C) iguais … iguais
(D) iguais … diferentes
- Opção (D)
⇒ O sinal sonoro tem a mesma frequência da fonte, o altifalante que por que o produziu.
⇒ Esta frequência não se altera devido ao meio em que se propaga e, portanto o sinal recebido pelo microfone tem a mesma frequência.
⇒ A intensidade depende energia do sinal transporta em cada ponto.
⇒ A onda sonora propaga-se em três dimensões, transferindo energia progressivamente para as camadas de ar à medida que se afasta do altifalante.
- Assim, o som vai diminuindo de intensidade com a distância altifalante.
- Opção (D) ……………. 7 pontos
6. (2020 – 2ªF) As baleias comunicam através de sons que podem ser registados por hidrofones (sensores de pressão) e por sismómetros (sensores de velocidade) instalados no fundo do mar.
Algumas baleias emitem um som com uma frequência praticamente constante, designado backbeat.
Na Figura 3, apresenta-se o registo de um sinal elétrico, obtido por um hidrofone, de parte de um backbeat.
No eixo horizontal representa-se o tempo em ms.
A frequência deste backbeat está contida no intervalo
(A) [36, 39] Hz
(B) [8, 11] Hz
(C) [53, 56] Hz
(D) [17, 20] Hz
- Opção (D)
⇒ A escala temporal apresenta 10 divisões entre os 200 ms e os 400 ms, assim cada divisão equivale a 20 ms.
⇒ Entre os 220 ms e os 300 ms decorre aproximadamente um período e meio.
Ou seja, a 4 divisões, 80 ms, corresponde aproximadamente 1,5 T donde se conclui que o período é próximo de 80 ms/1,5 = 53 ms e a frequência, f = 1/T, será próxima de 1/0,053 s = 19 Hz
ou
⇒ Na figura 3 do enunciado verifica-se que ao intervalo de tempo de 200 ms a 400 ms correspondem cerca de 3,5 períodos.
Assim,
- 400 – 200 = 3,5 T ⇔ T = 57,1 x 10-3 s
Como f = 1/T, então:
- Este valor, 17,5 Hz, está contido no intervalo [17, 20] Hz
- Opção (D) ……………. 10 pontos
7. (2020 – EE) O gráfico da Figura 4 representa um sinal elétrico, recebido num osciloscópio, em que a base de tempo foi regulada para 0,5 ms/div e o amplificador vertical para 0,2 V/div.
A frequência do sinal é e a amplitude do sinal é .
(A) 0,50 kHz … 0,40 V
(B) 0,50 kHz … 0,80 V
(C) 2,0 kHz … 0,40 V
(D) 2,0 kHz … 0,80 V
- Opção (A)
⇒ De acordo com as escalas definidas para o osciloscópio, cada divisão vertical corresponde a 0,2 V, logo a amplitude do sinal é 0,4 V, já que a altura de um pico corresponde a duas divisões.
⇒ A separação temporal entre dois máximos do sinal ( ou dois mínimos) corresponde ao período do sinal.
Deste modo, o período é igual a 2,0 ms (quatro divisões, 2,0 ms = 0,5 ms x 4).
- A frequência é o inverso do período f = 0,50 kHz.
ou
⇒ De acordo com o gráfico da Figura 4 e sendo a base de tempo registada para 0,5 ms/div, o período do sinal, T = 4 x 0,5 = 2,0 ms
- Como, f = 0,50 kHz
⇒ Como a amplitude vertical foi regulada para 0,2 V/div (o que indica que o valor da tensão correspondente a cada divisão da escala vertical do ecrã é 0,2 V) e a deflexão vertical foi de duas divisões, a tensão será 2 x 0,2 V = 0,4 V
- A amplitude do sinal é 0,4 V
- Opção (A) ……………. 10 pontos
8. (2021 – 1ªF) Dois microfones idênticos, ligados a um osciloscópio, foram colocados à mesma distância de um altifalante.
A Figura 6 apresenta os sinais I e II, visualizados no ecrã do osciloscópio, quando a base de tempo foi regulada para 0,5 ms por divisão e o amplificador vertical foi regulado para 0,5 V por divisão (para os dois sinais).
8.1. A frequência do sinal I é ______ e a amplitude desse sinal é ______ amplitude do sinal II.
(A) 3,0 x 102 Hz … igual
(B) 3,3 x 103 Hz … igual
(C) 3,0 x 102 Hz … inferior
(D) 3,3 x 103 Hz … inferior
- Opção (A)
⇒ A frequência do sinal I é 3,0×102 Hz e a amplitude desse sinal é igual à amplitude do sinal II.
Notas:
⇒ O intervalo de tempo referente ao sinal apresentado no ecrã do osciloscópio corresponde a um período e meio.
Como a base de tempo está regulada para 0,5 ms/DIV, pode concluir-se que
- 0,5 × 10−3 s/DIV × 10 DIV = 1,5 × 𝛵 ⇔ 𝛵 = 5 × 10−3 s/ 1,5
⇒ Sendo a frequência por definição o inverso do período, vem:
- 𝑓 = 1/𝛵 = 1,5 / 5 × 10−3 s ⇔ 𝑓 = 3,0 × 102 Hz
⇒ Observando a imagem do ecrã do osciloscópio, pode concluir- -se que a distância pico a pico do sinal I é aproximadamente igual à do sinal II, pelo que se pode afirmar que a amplitude do sinal I é igual à do sinal II, o que corresponde ao esperado, pois os dois microfones foram colocados à mesma distância de um altifalante.
- Opção (A) ……………. 10 pontos
8.2. O microfone que originava o sinal II foi afastado do altifalante de uma distância igual a um quarto do comprimento de onda da onda sonora produzida pelo altifalante.
Qual das opções seguintes apresenta os sinais que seriam observados no ecrã do osciloscópio, após o ajuste do sinal II ao ecrã do osciloscópio?
- Opção (C)
A SPF concluiu que nenhum dos gráficos está correto, porque o afastamento do microfone que originava o sinal II de um quarto de comprimento de onda implica que este deveria estar atrasado de um quarto de período relativamente ao sinal I, isto é, o pico do sinal II deveria aparecer à direita do pico do sinal I.
Estando o microfone que originava o sinal II mais longe, o sinal nele detetado num certo instante é um sinal emitido pelo altifalante antes do sinal que está nesse mesmo instante a ser detetado pelo outro microfone. É esta a razão para o desfasamento. Além disso, há atenuação do sinal II que está bem refletida na opção C.
- Opção (C) ……………. 10 pontos
9. (2021 – EE) Considere uma onda transversal e sinusoidal que se propaga num lago onde se encontra uma boia de sinalização, B.
Na Figura 5 (que não está à escala), representa-se uma porção da superfície da água do lago, num dado instante, ti , e um referencial xOy.
Admita que a onda se propaga no sentido positivo do eixo Ox com velocidade constante.
Qual dos esboços de gráfico seguintes pode representar a componente escalar da posição da boia de sinalização, yB , segundo o eixo Oy, em função do tempo, t , considerando ti o instante inicial?
- Opção (A)
⇒ Da Figura, verifica-se que a boia no instante ti se encontra na posição de equilíbrio (y = 0).
⇒ No instante ti, a partícula que se encontra no eixo dos tem elongação máxima negativa, pelo que, no instante ti + T/4, passa na posição y = 0 ; assim, a porção da água do lago para este instante é a representada (a tracejado) na figura seguinte:
⇒ Nesta figura, verifica-se que a boia se encontra na elongação máxima negativa.
- Opção (A) ……………. 10 pontos
10. (2022 – 1ªF) Para prever erupções vulcânicas, os cientistas monitorizam a atividade sísmica com sismógrafos.
Os sismos geram, entre outros tipos de ondas, ondas transversais, S, e ondas longitudinais, P.
O epicentro de um sismo ocorre a 3220 km de uma estação sismográfica, sendo as ondas S detetadas 4,8 minutos depois das ondas P.
Admita uma propagação em linha reta e considere que as velocidades das ondas P e S se mantêm constantes durante o percurso.
A velocidade de propagação das ondas P é 8,0 km s-1. Qual é a velocidade de propagação das ondas S?
(A) 7,9 km s-1
(B) 3,2 km s-1
(C) 4,7 km s-1
(D) 11,2 km s-1
- Opção (C)
⇒ A velocidade de propagação das S é 4,7 km s-1
Notas:
⇒ A velocidade de propagação das ondas sísmicas num meio homogéneo é calculada usando a expressão:
⇒ Considerando as ondas longitudinais, P, temos:
⇒ A velocidade de propagação das ondas
- Opção (C) ……………. 10 pontos
11. (2022 – 1ªF) A queda vertical da pedra na superfície da água origina uma onda circular, tal como se representa na Figura 6.
Na imagem, as zonas mais claras correspondem a cristas, e as zonas mais escuras correspondem a vales.
Admita um diâmetro, D, de 3,0 m.
Entre o instante em que a pedra atinge a água e o instante em que a frente de onda atinge a margem, o intervalo de tempo decorrido é 3,0 s.
A onda que se propaga na água tem
(A) uma frequência de 3,3 Hz.
(B) um comprimento de onda de 0,6 m.
(C) uma frequência de 1,7 Hz.
(D) um comprimento de onda de 1,0 m.
- Opção (C)
⇒ A onda que se propaga na água tem uma frequência de 1,7 Hz
Notas:
⇒ Cálculo do comprimento de onda:
- D = 10 x λ ⇔ 3,0 = 10 x λ ⇔ λ = 0,30 m
⇒ Cálculo da velocidade de propagação da onda na água:
⇒ Cálculo da frequência:
- v = λ x f ⇔ 0,50 = 0,30 x f ⇔ f = 1,7 Hz
- Opção (C) ……………. 10 pontos
