2012 – 1ª Fase – Prova Escrita de Física e Química A

Prova Escrita de Física e Química A – versão 1

Prova 715: 1.ª Fase – 2012

Grupo I

Um átomo é formado quase completamente por espaço vazio. Toda a sua massa se deve ao diminuto núcleo central. O espaço que o rodeia estende-se até uma distância de cerca de 10 mil vezes o diâmetro do núcleo e é ocupado por uma mão-cheia de eletrões – seis, por exemplo, no caso do átomo de carbono.

O vazio extranuclear é, porém, a sede da personalidade de um elemento – o núcleo é um observador passivo, responsável por dirigir o conjunto de eletrões em seu redor, dos quais apenas alguns participam nas reações químicas.

Os cientistas não puderam resistir à tentação de supor que os eletrões eram como planetas para o núcleo-estrela. No entanto, este modelo planetário, adotado, entre outros, por Niels Bohr, estava errado. A verificação de que os eletrões não são apenas partículas no sentido comum, mas possuem também um carácter ondulatório intrínseco, permite atribuir-lhes um carácter duplo, que implica que seja totalmente inapropriado visualizar os eletrões como partículas em órbitas bem definidas.

Por volta de 1926, Erwin Schrödinger desenvolveu uma equação que, quando resolvida, permite obter informação acerca do comportamento dos eletrões nos átomos. As soluções desta equação permitem calcular a probabilidade de encontrar o eletrão numa dada região do espaço e não a sua localização precisa em cada instante, como na física clássica.

P. Atkins, O Dedo de Galileu – As dez grandes ideias da Ciência, Gradiva, 1.ª ed., 2007 (adaptado)

10ºano – Química – Domínio 2 – subdomínio 1 (Ligação química)

1. Como se designam os eletrões que participam nas reações químicas?

Resolução

Eletrões de valência.

⇒ As propriedades químicas dos elementos dependem fundamentalmente dos eletrões da última camada – eletrões de valência – que os átomos utilizam no estabelecimento de ligações químicas.

Critérios

Eletrões de valência …………. 5 pontos

10ºano – Química – Domínio 1 – subdomínio 2 (Energia dos eletrões nos átomos)

2. Qual das configurações eletrónicas seguintes pode corresponder a um átomo de carbono no estado fundamental?

(A) 1s² 2s¹ 2p_x¹ 2p_y¹ 2p_z¹

(B) 1s² 2s² 2p_x¹ 2p_y⁰ 2p_z¹

(C) 1s² 2s² 2p_x²

(D) 1s² 2s¹ 2p_x² 2p_y¹

Resolução

Opção (B)

⇒ Como o número atómico do carbono é 6 o átomo de carbono tem 6 eletrões.

⇒ De acordo com o princípio de energia mínima, os eletrões ficam distribuídos sucessivamente pelas orbitais 1s, 2s e 2p (2p_x 2p_y 2p_z) e cada orbital pode ter no máximo 2 eletrões.

⇒ Distribuindo os 6 eletrões pelas orbitais de menor energia obtém-se a seguinte configuração 1s² 2s² 2p².

⇒ Existem três orbitais 2p degeneradas, sendo a energia mínima para a configuração em que os 2 eletrões nas orbitais 2p estão em diferentes orbitais tal como, por exemplo, na opção (B):

1s² 2s² 2p_x¹ 2p_y⁰ 2p_z¹

Critérios

Opção (B)…………. 5 pontos

10ºano – Química – Domínio 1 – subdomínio 1 (Massa e tamanho dos átomos)

3. Os átomos dos isótopos 12 e 13 do carbono têm

(A) números atómicos diferentes.

(B) números de massa iguais.

(C) igual número de eletrões.

(D) igual número de neutrões.

Resolução

Opção (C)

⇒ Os isótopos ¹²C e ¹³C s o átomos do mesmo elemento e, portanto, com o mesmo número atómico Z.

⇒ Diferem no número de massa, A, por terem diferente número de neutrões.

⇒ Por exemplo, os átomos dos isótopos ¹²C e ¹³C têm o mesmo número atómico (Z = 6), isto é, 6 protões no núcleo e 6 eletrões e diferente número de massa (A = 12 para o isótopo com 6 neutrões no núcleo e A = 13 para o que tem 7 neutrões no núcleo).

Critérios

Opção (C)…………. 5 pontos

10ºano – Química – Domínio 1 – subdomínio 2 (Energia dos eletrões nos átomos)

4. Como se designa uma região do espaço onde, em torno do núcleo de um átomo, existe uma elevada probabilidade de encontrar um eletrão desse átomo?

Resolução

⇒ Orbital (atómica) é a zona do espaço em torno do núcleo de um átomo onde é elevada a probabilidade de se encontrar um eletrão (de um átomo) com uma dada energia.

Critérios

Orbital [atómica] …………. 5 pontos

Grupo II

1. O sulfureto de hidrogénio, H₂S (g), é um gás incolor que tem um cheiro característico a ovos podres.

10ºano – Química – Domínio 2 – subdomínio 2 (Gases e dispersões)

1.1. A tabela seguinte apresenta os volumes, V, de diferentes amostras de H₂S (g) e as respetivas massas, m, à pressão de 1 atm e à temperatura de 55 ºC.

Determine o volume molar do gás, nas condições de pressão e de temperatura referidas.

Comece por obter a densidade (ou massa volúmica) do gás, a partir do declive da reta que melhor se ajusta ao conjunto de valores apresentados na tabela (utilize a calculadora gráfica).

Apresente todas as etapas de resolução.

Resolução

⇒ Analisando gráfica e estatisticamente os dados da tabela obtém-se o gráfico seguinte e a reta de ajuste da massa (m) de H₂S em função do volume (V):

m = 1,267 V + 1 x 10^–4 m ≈ 1,267 V

Como m = ρ V , conclui-se que a massa volúmica é ρ = 1,267 g dm^–3. ⇒ Cálculo da massa molar de H₂S:

M(H₂S) = 2 x 1,01 + 32,07 = 34,09 g mol^–1

⇒ Obtenção da relação entre o volume molar e a densidade de um gás:

⇒ Cálculo do volume molar do gás à pressão de 1 atm e à temperatura de 55 ºC:

Critérios

A resolução deve apresentar as seguintes etapas:

A) Cálculo da densidade (ou massa volúmica) do gás (ρ = 1,267 g dm^-3).

B) Cálculo do volume molar do gás, nas condições de pressão e de temperatura referidas (Vm = 26,9 dm³ mol^-1).

A resposta a este item deve ser enquadrada num dos níveis de desempenho relacionados com a consecução das etapas, de acordo com a tabela seguinte.

A classificação a atribuir à resposta resulta da pontuação decorrente do enquadramento num dos níveis de desempenho atrás descritos, à qual podem ser subtraídos pontos, de acordo com o enquadramento nos níveis de desempenho relacionados com o tipo de erros cometidos.

10ºano – Química – Domínio 2 – subdomínio 2 (Gases e dispersões)

1.2. Considere uma amostra de H₂S (g) com o dobro do volume de uma amostra de metano, CH₄ (g), nas mesmas condições de pressão e de temperatura.

Nessas condições, as amostras contêm

(A) o mesmo número de moléculas.

(B) a mesma quantidade de moléculas.

(C) o mesmo número de átomos de hidrogénio.

(D) a mesma quantidade de átomos.

Resolução

Opção (C)

⇒ De acordo com a lei de Avogadro, no dobro do volume existem, nas mesmas condições de pressão e temperatura, o dobro da quantidade de matéria e, em consequência, o dobro do número de moléculas.

⇒ Como cada molécula de H₂S tem metade do número de átomos de hidrogénio em relação à molécula CH₄, conclui-se que o número de átomos de hidrogénio é o mesmo nas duas amostras.

Critérios

Opção (C)…………. 5 pontos

11ºano – Química – Domínio 2 – subdomínio 1 (Reações ácido-base)

1.3. O H₂S (g) libertado pelos vulcões reage, a temperaturas elevadas, com o oxigénio do ar, formando-se dióxido de enxofre, SO₂ (g), e água, H₂O (g).

Escreva a equação química que traduz esta reação e justifique o facto de a emissão de SO₂ (g) para a atmosfera contribuir para o aumento da acidez da água da chuva.

Resolução

2 H₂S (g) + 3 O₂ (g) → 2 SO₂ (g) + 2 H₂O (g)

⇒ O SO₂ (g) emitido para a atmosfera reage com a água originando soluções ácidas.

⇒ Parte do dióxido de enxofre (SO₂) é oxidado a trióxido de enxofre (SO₃).

⇒ Estes óxidos, por reação com a água contida na atmosfera ou com a água da chuva, originam ácido sulfuroso, H₂SO₃ (aq), e ácido sulfúrico, H₂SO₄ (aq), respetivamente.

SO₂ (g) + H₂O (l) → H₂SO₃ (aq)
SO₃ (g) + H₂O (l) → H₂SO₄ (aq)

⇒ A existência destes ácidos na água da chuva contribui para o aumento da sua acidez relativamente à acidez natural (devida ao dióxido de carbono atmosférico).

Critérios

A resposta deve apresentar os seguintes tópicos:

A) 2 H₂S (g) + 3 O₂ (g) → 2 SO₂ (g) + 2 H₂O (g)

B) A emissão de SO₂ (g) para a atmosfera implica a ocorrência de reações com a água [na atmosfera] que originam ácidos [, que contribuem para o aumento da acidez da água da chuva].

A classificação da resposta a este item é feita em função do enquadramento da mesma num dos níveis de desempenho, de acordo com a tabela seguinte.

2. O sulfureto de hidrogénio dissolve-se em água, dando origem ao ácido sulfídrico, H₂S (aq).

10ºano – Química – Domínio 2 – subdomínio 2 (Gases e dispersões)

2.1. Se o teor de sulfureto de hidrogénio numa solução aquosa for 22 ppm, a massa, expressa em mg, de H₂S em 1 kg dessa solução é

(A) 22 x 10⁶

(B) 22

(C) 22 x 10^-3

(D) 22 x 10³

Resolução

Opção (B)

então há 22 mg de H₂S por cada kg de solução

Critérios

Opção (B)…………. 5 pontos

11ºano – Química – Domínio 2 – subdomínio 2 (Reações de oxidação redução)

2.2. O mau cheiro de uma solução contendo H₂S (aq) pode ser removido pela adição de cloro, Cl₂ (aq), a essa solução.

A reação que ocorre é traduzida por

H₂S (aq) + Cl₂ (aq) → S (s) + 2 HCl (aq)

Nesta reação, o agente redutor é o

(A) H₂S (aq) que é oxidado pelo Cl₂ (aq).

(B) Cl₂ (aq) que é oxidado pelo H₂S (aq).

(C) H₂S (aq) que é reduzido pelo Cl₂ (aq).

(D) Cl₂ (aq) que é reduzido pelo H₂S (aq).

Resolução

Opção (A)

⇒ Nesta reação, o H₂S (aq) é oxidado pelo Cl₂ (aq).

⇒ O número de oxidação do elemento S passa de – 2 em H₂S para zero em S (s).

⇒ Aumenta o número de oxidação, Δn.o. = 0 – (-2) = +2, logo ocorre uma oxidação.

A espécie H₂S atua como redutor.

Critérios

Opção (A)…………. 5 pontos

3. O ácido sulfídrico, H₂S (aq), é um ácido diprótico muito fraco.

A reação deste ácido com a água pode ser traduzida por

H₂S (aq) + 2 H₂O (l) ⇋ S^2– (aq) + 2 H₃O⁺ (aq)

A constante de acidez do H₂S (aq), definida para a reação anterior, é 6,8 x 10^–23, a 25 ºC.

3.1. A uma dada temperatura, o ácido sulfídrico

(A) ioniza-se tanto mais quanto menor for o pH do meio.

(B) ioniza-se tanto mais quanto maior for o pH do meio.

(C) dissocia-se tanto mais quanto maior for o pH do meio.

(D) dissocia-se tanto mais quanto menor for o pH do meio.

*O conteúdo deste item já não faz parte dos atuais referenciais programáticos da disciplina.

Resolução

Opção (B)

⇒ A ionização do ácido sulfídrico é favorecida por uma menor concentração do ião hidrónio (segundo o princípio de Le Châtelier, o sistema evolui no sentido de repor esses iões, ou seja, no sentido direto, originando maior ionização do ácido).

Quanto menor a concentração de H₃O⁺, maior o pH.

Critérios

Opção (B)…………. 5 pontos

11ºano – Química – Domínio 2 – subdomínio 3 (Soluções e equilíbrio de solubilidade)

3.2. O sulfureto de ferro, FeS, é um sal bastante insolúvel em água, cujo produto de solubilidade é 6,3 × 10^–18, a 25 ºC.

A precipitação deste sal, em solução aquosa, pode ser traduzida por

Fe²⁺(aq) + S^2– (aq) ⇋ FeS (s)

Admita que se pretende precipitar sulfureto de ferro a partir de uma solução que contém 4,47 g de ião Fe²⁺(aq) (M = 55,85 g mol^-1) por dm³, utilizando ácido sulfídrico de concentração 0,10 mol dm^–3, que é mantida constante ao longo da reação.

Determine a concentração hidrogeniónica necessária para que o sulfureto de ferro possa precipitar.

Apresente todas as etapas de resolução.

Resolução

Cálculo da concentração do ião ferro (II):

Determinação da concentração do ião sulfureto numa solução saturada de sulfureto de ferro (II):

Determinação da concentração do ião hidrônio em equilíbrio com o ião sulfureto numa solução de ácido sulfídrico:

⇒ Para concentrações hidrogeniónicas inferiores a 2,9 x 10^–4 mol dm^–3, irá ocorrer precipitação do sulfureto de ferro (II).

Critérios

A resolução deve apresentar as seguintes etapas:

A) Cálculo da concentração de ião Fe²⁺ (aq) (c = 8,00 x 10^–2 mol dm^–3).

B) Cálculo da concentração de ião S^2– (aq) (c = 7,88 x 10^–17 mol dm^–3).

C) Cálculo da concentração hidrogeniónica necessária para que o sulfureto de ferro possa precipitar ([H₃O⁺] = 2,9 x 10^–4 mol dm^–3).

A resposta a este item deve ser enquadrada num dos níveis de desempenho relacionados com a consecução das etapas, de acordo com a tabela seguinte.

10ºano – Química – Domínio 2 – subdomínio 1 (Ligação química)

4. As moléculas de H₂S e de H₂O têm ambas geometria angular, apresentando o mesmo número de eletrões de valência.

Na molécula de H₂S existem, no total, ______ eletrões de valência, sendo _______ deles não ligantes.

(A) oito … dois

(B) seis … quatro

(C) seis … dois

(D) oito … quatro

Resolução

Opção (D)

⇒ Cada átomo de hidrogénio tem 1 eletrão de valência. O átomo de enxofre é do grupo 16 logo tem 6 eletrões de valência. Assim, a molécula H₂S tem 2 x 1 + 6 = 8 eletrões de valência.

⇒ O enxofre estabelece ligações covalentes simples com os átomos de hidrogénio, restando 2 pares de eletrões não ligantes (4 eletrões).

Critérios

Opção (D)…………. 5 pontos

Grupo III

As curvas representadas no gráfico da Figura 1 traduzem a concentração, c, ao longo do tempo, t, das espécies A, B e C que intervêm numa reação química em fase gasosa. O sistema químico atinge um estado de equilíbrio a uma temperatura T.

11ºano – Química – Domínio 1 – subdomínio 2 (Equilíbrio químico)

1. Em que proporção reagem entre si as espécies A e B?

(A) 2 mol A : 1 mol B

(B) 3 mol A : 2 mol B

(C) 1 mol A : 2 mol B

(D) 2 mol A : 3 mol B

Resolução

Opção (D)

⇒ De acordo com o gráfico da figura 1, a concentração de A diminui 1,00 – 0,49 = 0,51 mol dm^-3 e a concentração de B diminui 1,00 – 0,23 = 0,77 mol dm^-3.

⇒ A proporção em que reagem entre si as espécies A e B é 0,51 (A) para 0,77 (B).

⇒ Como 0,51 / 0,77 = 0,66, esta proporção é aproximadamente de 2 mol de A para 3 mol de B.

Critérios

Opção (D)…………. 5 pontos

11ºano – Química – Domínio 1 – subdomínio 2 (Equilíbrio químico)

2. O instante a partir do qual se pode considerar que o sistema químico atinge um estado de equilíbrio é

(A) t₁

(B) t₂

(C) t₃

(D) t₄

Resolução

Opção (C)

⇒ O equilíbrio químico é atingido quando não há mais variação na concentração das espécies, sendo t₃ o instante a partir do qual isso se verifica.

Critérios

Opção (C)…………. 5 pontos

11ºano – Química – Domínio 1 – subdomínio 2 (Equilíbrio químico)

3. Considere que num determinado instante, depois de atingido o estado de equilíbrio à temperatura T, se aumenta a concentração da espécie A.

Conclua, justificando, como variará o quociente da reação, após o aumento da concentração da espécie A, até ser atingido um novo estado de equilíbrio, à mesma temperatura.

Resolução

⇒ Quando se aumenta a concentração da espécie A depois de atingido o estado de equilíbrio, o quociente da reação diminui já que, de acordo com o gráfico, A é um reagente.

⇒ De acordo com o princípio de Le Châtelier, o aumento da concentração da espécie A favorece a reação direta.

⇒ Assim, as concentrações dos reagentes diminuem e a do produto da reação aumenta até ser atingido um novo estado de equilíbrio.

⇒ Conclui-se que o quociente da reação irá aumentar até que volte a igualar a constante de equilíbrio à temperatura T.

Critérios

A resposta deve apresentar os seguintes tópicos:

A) De acordo com o Princípio de Le Châtelier, o aumento da concentração da espécie A favorece a reação direta.

B) Assim, o quociente da reação irá aumentar [até igualar o valor da constante de equilíbrio da reação à temperatura T ].

A classificação da resposta a este item é feita em função do enquadramento da mesma num dos níveis de desempenho, de acordo com a tabela seguinte.

Grupo IV

Com o objetivo de determinar a capacidade térmica mássica do cobre e do alumínio, um grupo de alunos utilizou sucessivamente blocos calorimétricos desses metais, numa montagem semelhante à representada na Figura 2.

Os alunos começaram por introduzir um sensor de temperatura, ligado a um sistema de aquisição de dados, num dos orifícios de um desses blocos calorimétricos e uma resistência de aquecimento no outro orifício.

Tiveram, ainda, o cuidado de proceder de modo a otimizar o contacto térmico do bloco, quer com o sensor, quer com a resistência, e a minimizar a taxa de dissipação de energia do bloco.

Seguidamente, os alunos montaram um circuito elétrico, ligando a resistência de aquecimento a uma fonte de alimentação, a um voltímetro, a um amperímetro e a um interruptor.

10ºano – Física – subdomínio 2 (Energia e fenómenos elétricos)
10ºano – Física – subdomínio 3 (Energia, fenómenos térmicos e radiação)

1. Qual dos esquemas seguintes pode representar o circuito elétrico montado pelos alunos?

Resolução

Opção (B)

⇒ O esquema que pode representar o circuito montado é o representado em (B), uma vez que (para medir a intensidade da corrente que percorre o circuito) o amperímetro terá de ser ligado em série enquanto (para medir a diferença de potencial entre os terminais da resistência de aquecimento) o voltímetro terá de ser ligado em paralelo.

Critérios

Opção (B)…………. 5 pontos

2. Os alunos ligaram o interruptor do circuito elétrico e iniciaram, simultaneamente, o registo da temperatura do bloco de cobre em função do tempo.

10ºano – Física – subdomínio 2 (Energia e fenómenos elétricos)
10ºano – Física – subdomínio 3 (Energia, fenómenos térmicos e radiação)

2.1. Identifique uma das grandezas que os alunos tiveram de medir para calcularem a potência dissipada pela resistência de aquecimento.

Resolução

⇒ A diferença de potencial ou a intensidade da corrente elétrica.

⇒ Para calcularem a potência dissipada pela resistência de aquecimento, os alunos tiveram de recorrer à lei de Joule, P = I U, pelo que tiveram de medir a diferença de potencial, U, entre os terminais da resistência e a intensidade da corrente elétrica, I, que percorre o circuito.

Critérios

Diferença de potencial ou Tensão ou Intensidade de corrente …………. 8 pontos

10ºano – Física – subdomínio 3 (Energia, fenómenos térmicos e radiação)

2.2. A potência dissipada pela resistência de aquecimento na experiência realizada foi 1,58 W.

A Figura 3 apresenta o gráfico da temperatura do bloco de cobre, de massa 1,00 kg, em função do tempo.

Determine, a partir dos resultados da experiência, o valor da capacidade térmica mássica do cobre.

Apresente todas as etapas de resolução.

Resolução

P = 1,58 W;
m = 1,00 kg

⇒ Para determinar o valor da capacidade térmica mássica recorre-se à expressão:

E = m c ΔT

sendo E a energia fornecida pela resistência de aquecimento ao bloco de cobre durante um dado intervalo de tempo, Δt, e ΔT a variação de temperatura experimentada durante este intervalo de tempo.

⇒ Como E = P Δt, pode escrever-se:

P Δt = m c ΔT

⇒ Os valores de Δt e de ΔT obtém-se recorrendo ao gráfico da temperatura em função do tempo.

⇒ O intervalo de tempo a considerar terá obrigatoriamente que corresponder à variação linear do gráfico (a partir de t = 30 s).

Assim, por exemplo, tem-se para Δt = 140 – 40 = 100 s, Δθ = 17,90 – 17,52 = 0,38 ºC.

Δθ = ΔT ⇒ ΔT = 0,38 K

Substituindo em (1)

⇒ A capacidade térmica mássica do cobre à igual a 4,16 x 10² J kg^-1 ºC^-1.

Critérios

A resolução deve apresentar as seguintes etapas:

A) Determinação de uma variação de temperatura do bloco de cobre coerente com o intervalo de tempo considerado (Δθ = 0,38 ºC para Δt = 100 s).

B) Cálculo da capacidade térmica mássica do cobre (c = 4,16 x 10² J kg^–1 ºC^–1).

A resposta a este item deve ser enquadrada num dos níveis de desempenho relacionados com a consecução das etapas, de acordo com a tabela seguinte.

10ºano – Física – subdomínio 3 (Energia, fenómenos térmicos e radiação)

3. Seguidamente, os alunos repetiram a experiência, nas mesmas condições, substituindo apenas o bloco de cobre por outro de alumínio, aproximadamente com a mesma massa.

A Figura 4 apresenta o esboço dos gráficos da temperatura de cada um dos blocos, em função do tempo.

Conclua, justificando, qual dos dois metais, cobre ou alumínio, terá maior capacidade térmica mássica.

Resolução

⇒ A capacidade térmica mássica de uma substância é, para a mesma energia e massa, inversamente proporcional à variação de temperatura ocorrida.

⇒ Num mesmo intervalo de tempo é fornecida a mesma energia aos blocos de cobre e ao alumínio. Ora, para um determinado intervalo de tempo, ou seja para a mesma energia, a variação de temperatura do alumínio é menor.

⇒ Logo o alumínio tem maior capacidade térmica mássica.

Critérios

A resposta deve apresentar os seguintes tópicos:

A) Num mesmo intervalo de tempo, a variação da temperatura do bloco de cobre é superior à variação da temperatura do bloco de alumínio.

B) Conclui-se, assim, que o alumínio terá maior capacidade térmica mássica [do que o cobre].

A classificação da resposta a este item é feita em função do enquadramento da mesma num dos níveis de desempenho, de acordo com a tabela seguinte.

Grupo V

Um carrinho de brincar desloca-se sobre uma pista que pode ser montada com diferentes formatos.

1. Considere que a pista é montada de modo que o carrinho descreva sobre ela uma trajetória circular, num mesmo plano horizontal, com velocidade de módulo constante.

11ºano – Física – Domínio 1 – subdomínio 3 (Forças e movimentos)

1.1. Caracterize os vetores velocidade e aceleração do carrinho quanto à sua direção e quanto ao seu sentido, relativamente à trajetória descrita.

Resolução

Como o carrinho descreve uma trajetória circular com velocidade de módulo constante está animado de movimento circular uniforme.

⇒ O vetor velocidade do carrinho tem, em cada instante, direção tangente à trajetória e sentido do movimento e o vetor aceleração tem, em cada instante, direção perpendicular à trajetória (radial) e sentido para o centro da trajetória (centrípeto).

Critérios

A resposta deve apresentar os seguintes tópicos:

A) O vetor velocidade [do carrinho] tem direção tangente à trajetória [em cada ponto] e sentido do movimento OU equivalente.

B) O vetor aceleração [do carrinho] tem direção perpendicular à trajetória [em cada ponto] e sentido para o centro da trajetória OU equivalente.

A classificação da resposta a este item é feita em função do enquadramento da mesma num dos níveis de desempenho, de acordo com a tabela seguinte.

11ºano – Física – Domínio 1 – subdomínio 3 (Forças e movimentos)

1.2. Considere que a trajetória circular descrita pelo carrinho tem 50,0cm de diâmetro e que o carrinho demora, em média, 47,6 s a descrever 5 voltas completas.

Determine o módulo da aceleração do carrinho.

Apresente todas as etapas de resolução.

Resolução

Processo de resolução 1

⇒ Cálculo do período do movimento:

⇒ Cálculo do raio da trajetória:

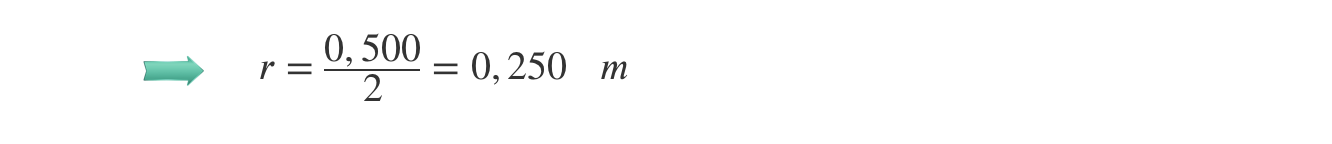
⇒ Obtenção da relação entre o módulo da aceleração, o período do movimento e o raio da circunferência descrita:

Determinação da aceleração do carrinho:

Processo de resolução 2

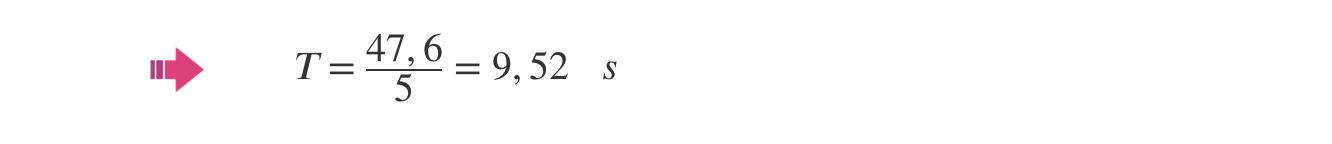⇒ Cálculo do período do movimento:

⇒ Cálculo do raio da trajetória:

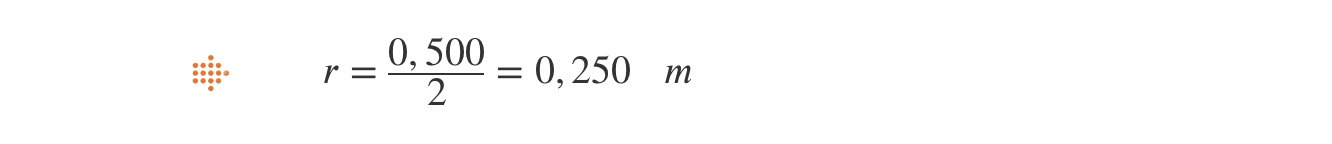
⇒ Cálculo do módulo da velocidade do carrinho:

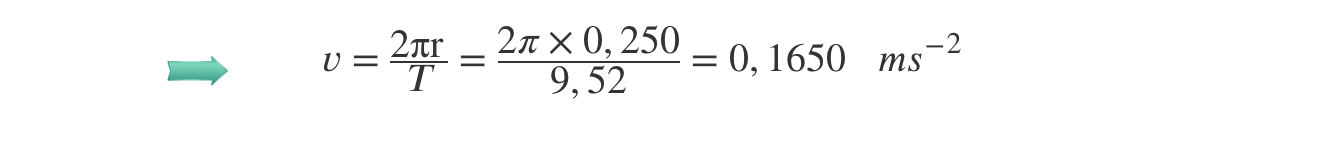⇒ Determinação da aceleração do carrinho:

Critérios

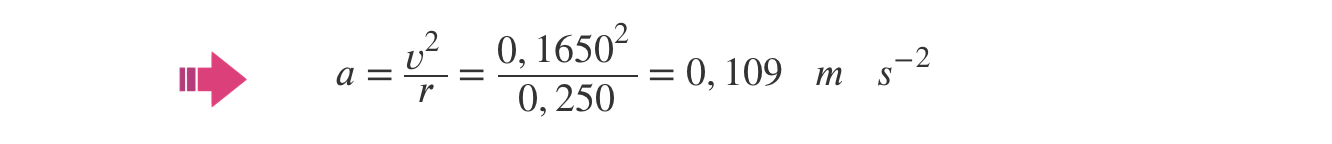
A resolução deve apresentar as seguintes etapas:

A) Cálculo do módulo da velocidade do carrinho (v = 1,650 x 10^–1 m s^–1).

Cálculo do módulo da velocidade angular do carrinho (ω = 6,600 x 10^–1 rad s^–1).

B) Cálculo do módulo da aceleração do carrinho (a = 1,09 x 10^–1 m s^–2).

A resposta a este item deve ser enquadrada num dos níveis de desempenho relacionados com a consecução das etapas, de acordo com a tabela seguinte.

11ºano – Física – Domínio 1 – subdomínio 3 (Forças e movimentos)

1.3. Admita que se colocaram sobrecargas de massa sucessivamente maior no carrinho e que os conjuntos carrinho + sobrecarga se deslocaram sobre a pista demorando o mesmo tempo a descrever uma volta completa.

Qual das opções seguintes apresenta os esboços dos gráficos que podem representar corretamente o módulo da aceleração, a, dos conjuntos carrinho + sobrecarga e a intensidade da resultante das forças neles aplicadas, F, em função da massa, m, daqueles conjuntos?

Resolução

Opção (A)

⇒ Como o período do movimento e o raio da trajetória são constantes, o módulo da aceleração não se altera com o aumento da massa, pois só depende destas grandezas:

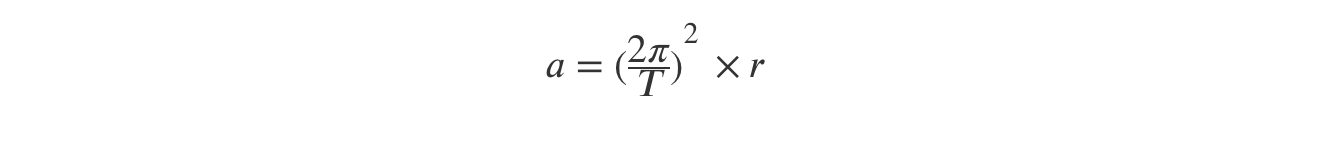pelo que as opções (C) e (D) são eliminadas.

⇒ De acordo com a 2.ª lei de Newton, a intensidade da resultante das forças que atuam sobre o sistema, F_R = m a, é diretamente proporcional à sua massa, logo a opção (B) é eliminada.

⇒ De acordo com o referido, a opção que apresenta os esboços de gráficos que podem representar a = f(m) e F_R = f(m) é a (A).

Critérios

Opção (A)…………. 5 pontos

2. Considere que a pista é agora montada formando uma rampa sobre a qual o carrinho percorre trajetórias retilíneas no sentido descendente ou no sentido ascendente.

10ºano – Física – subdomínio 1 (Energia e movimentos)

2.1. Na Figura 5, apresenta-se o esboço do gráfico que pode representar a soma dos trabalhos realizados pelas forças aplicadas no carrinho, W, em função da distância, d, percorrida pelo carrinho, à medida que este desce a rampa.

Qual é o significado físico do declive da reta representada?

Resolução

⇒ O declive da reta corresponde à intensidade da resultante das forças aplicadas no carrinho.

⇒ (O movimento retilíneo de descida da rampa é acelerado (a soma dos trabalhos é positiva), logo, o trabalho da resultante das forças pode ser escrito do seguinte modo:

W = F_R d cos 0º ⇔ W = F_R d

⇒ Da expressão anterior conclui-se que a intensidade da força resultante, considerada constante, é igual ao declive do gráfico da soma dos trabalhos em função da distância W = W (d) ).

Critérios

Intensidade da resultante das forças [aplicadas no carrinho] …………. 5 pontos

10ºano – Física – subdomínio 1 (Energia e movimentos)

2.2. Conclua, justificando, se existe conservação da energia mecânica do sistema carrinho +Terra quando o carrinho sobe a rampa com velocidade constante.

Resolução

⇒ Como a velocidade é constante não há variação de energia cinética (Ec = 0).

⇒ Quando o carrinho sobe, a energia potencial gravítica do sistema carrinho + Terra aumenta, ou seja, a variação de energia potencial é positiva (Ep > 0).

⇒ Em consequência, a energia mecânica do carrinho, soma das energias cinética e potencial gravítica, terá de aumentar (Ec + Ep = Em > 0).

⇒ Portanto, não há conservação de energia mecânica (a energia mecânica do sistema não é constante).

Critérios

A resposta deve apresentar os seguintes tópicos:

A) A energia cinética do carrinho mantém-se constante [quando o carrinho sobe a rampa], uma vez que a sua velocidade é constante.

B) A energia potencial gravítica do sistema carrinho + Terra varia [quando o carrinho sobe a rampa], uma vez que a altura varia.

C) Sendo a energia mecânica a soma das energias cinética e potencial gravítica, conclui-se que não existe conservação da energia mecânica do sistema carrinho + Terra [quando o carrinho sobe a rampa com velocidade constante].

A classificação da resposta a este item é feita em função do enquadramento da mesma num dos níveis de desempenho, de acordo com a tabela seguinte.

11ºano – Física – Domínio 2 – subdomínio 1 (Sinais e ondas)

3. A Figura 6 representa o espectro do som emitido pela buzina do carrinho.

O espectro representado permite concluir que o som emitido pela buzina do carrinho é

(A) puro, resultando da sobreposição de várias frequências.

(B) intenso, porque algumas das suas frequências são muito elevadas.

(C) harmónico, podendo ser descrito por uma função sinusoidal.

(D) complexo, resultando da sobreposição de vários harmónicos.

Resolução

Opção (D)

⇒ O gráfico mostra que o som emitido contém um conjunto diversificado de harmónicos. Trata-se, portanto, de um som complexo.

Critérios

Opção (D)…………. 5 pontos

Grupo VI

1. A Figura 7 representa parte do trajeto de um feixe de luz monocromática que se propaga no ar e que incide numa face de um paralelepípedo de vidro Flint, propagando-se depois no interior do vidro.

Os ângulos de incidência e de refração são, respetivamente, 24,0º e 16,0º.

11ºano – Física – Domínio 2 – subdomínio 3 (Ondas eletromagnéticas)

1.1. Determine a velocidade de propagação do feixe de luz monocromática no interior do vidro Flint.

Apresente todas as etapas de resolução.

n_ar (índice de refração do ar) = 1,00

Resolução

⇒ Aplicando a lei de Snell-Descartes para a refração obtém-se o índice de refração do vidro Flint:

⇒ A velocidade de propagação da luz neste vidro obtém-se a partir da relação entre o índice de refração e a velocidade da luz num determinado meio:

Critérios

A resolução deve apresentar as seguintes etapas:

A) Cálculo do índice de refração do vidro Flint para o feixe de luz monocromática considerado (n = 1,476).

B) Cálculo da velocidade de propagação do feixe de luz monocromática no interior do vidro Flint (v = 2,03 x 10⁸ m s^–1).

A resposta a este item deve ser enquadrada num dos níveis de desempenho relacionados com a consecução das etapas, de acordo com a tabela seguinte.

11ºano – Física – Domínio 2 – subdomínio 3 (Ondas eletromagnéticas)

1.2. Qual dos esquemas seguintes pode representar o trajeto do feixe de luz monocromática ao propagar-se do interior do vidro Flint novamente para o ar?

Resolução

Opção (B)

⇒ Um feixe de luz ao passar do ar para o vidro aproxima-se da normal à superfície de separação dos dois meios. Quando passa do vidro para o ar sucede o oposto: a luz afasta-se da normal.

⇒ Como a duas faces opostas do paralelepípedo são paralelas o ângulo de refração na passagem da luz do ar para o vidro é igual ao de incidência na passagem da luz do vidro para o ar.

⇒ Conclui-se que o feixe que sai para o ar deve ser paralelo ao feixe incidente no vidro.

Critérios

Opção (B)…………. 5 pontos

11ºano – Física – Domínio 2 – subdomínio 3 (Ondas eletromagnéticas)

2. A reflexão total da luz ocorre quando esta incide na superfície de separação entre um meio e outro de

(A) maior índice de refração, com um ângulo de incidência superior ao ângulo crítico.

(B) menor índice de refração, com um ângulo de incidência inferior ao ângulo crítico.

(C) maior índice de refração, com um ângulo de incidência inferior ao ângulo crítico.

(D) menor índice de refração, com um ângulo de incidência superior ao ângulo crítico.

Resolução

Opção (D)

⇒ A reflexão total ocorre quando a luz se propaga de um meio mais refringente para um menos refringente (com menor índice de refração).

⇒ Se o ângulo de incidência for superior ao ângulo crítico a luz não se propaga para o segundo meio ocorrendo o fenómeno de reflexão total.

Critérios

Opção (D)…………. 5 pontos

FIM

2012 – 1ª Fase – Prova Escrita de Física e Química A

Deixe um comentário Cancelar resposta

1468

2053

198

10

Receba novidades

Cursos

Links úteis

Utilizador