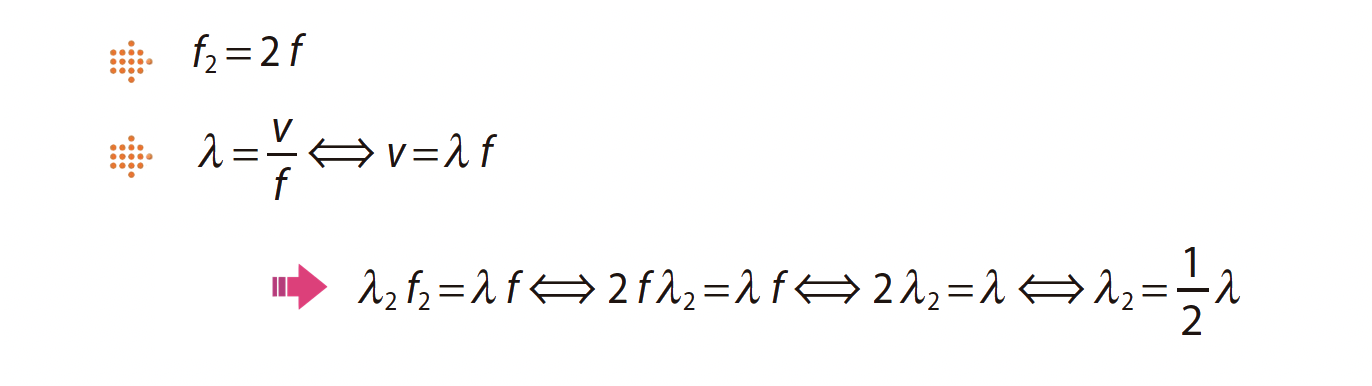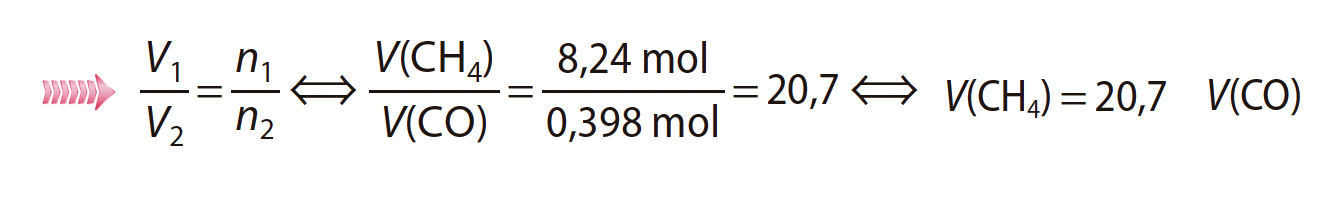2011 – 1ª Fase – Prova Escrita de Física e Química A

Prova Escrita de Física e Química A – versão 1

Prova 715: 1.ª Fase – 2011

Grupo I

Suponhamos que alguém vai a empurrar um carrinho por uma estrada retilínea e horizontal e que, subitamente, o larga.

Antes de se imobilizar, o carrinho ainda percorrerá uma curta distância. Surge a pergunta: como será possível aumentar essa distância? Há vários meios, como por exemplo, olear o eixo e tornar a estrada mais lisa.

Quanto mais lisa for a estrada e mais facilmente girarem as rodas, maior será a distância percorrida. O que acontece em consequência da lubrificação do eixo e do alisamento da estrada?

Apenas isto: o efeito do que chamamos atrito diminui, tanto no contacto do eixo com as rodas, como no das rodas com a estrada.

Isto já é uma interpretação teórica da evidência observável. Imaginemos uma estrada perfeitamente lisa e um sistema de eixos e rodas em que não houvesse atrito. Neste caso, nada interferiria no carrinho, que se moveria perpetuamente.

Formulamos esta conclusão unicamente por força do pensamento, idealizando uma experiência que não pode ter realidade, visto ser impossível eliminar o atrito, mas que nos permite compreender melhor a relação entre forças e movimento.

A. Einstein, L. Infeld, A Evolução da Física, Livros do Brasil (adaptado)

11ºano – Física – Domínio 1 – subdomínio 3 (Forças e movimentos)

1. «Neste caso, nada interferiria no carrinho, que se moveria perpetuamente.»

Qual seria o tipo de movimento do carrinho na situação descrita?

Resolução

⇒ “Numa estrada perfeitamente lisa e um sistema de eixos e rodas em que não houvesse atrito”, a intensidade das forças de atrito é desprezável.

⇒ A resultante de todas as forças, Fr, que atuam sobre o carrinho é:

→ Fg = – F_N

Fr = Fg + F_N ⇔ Fr = 0

⇒ Como a resultante das forças é nula, de acordo com a 1.ª lei de Newton, a velocidade do carrinho é constante, pelo que se deslocará animado de movimento retilíneo e uniforme.

Critérios

[Movimento] retilíneo uniforme. …………. 5 pontos

11ºano – Física – Domínio 1 – subdomínio 2 (Interações e os seus efeitos)

2. Das forças que atuam sobre o carrinho em movimento sobre uma superfície horizontal, a força gravítica, Fg, e a força normal, F_N, exercida pela estrada, são forças com intensidades

(A) iguais, que constituem um par ação-reação.

(B) diferentes, que constituem um par ação-reação.

(C) diferentes, que não constituem um par ação-reação.

(D) iguais, que não constituem um par ação-reação.

Resolução

Opção (D)

⇒ A força gravítica é exercida pela Terra e a força normal pela superfície horizontal.

⇒ Ambas atuam sobre o carrinho. Sendo aplicadas no mesmo corpo não constituem um par ação-reação.

⇒ Como estas duas forças se anulam são simétricas, portanto têm a mesma intensidade.

Critérios

Opção (D)…………. 5 pontos

11ºano – Física – Domínio 1 – subdomínio 3 (Forças e movimentos)

3. Fundamente a afirmação de Einstein e Infeld segundo a qual se pode aumentar a distância percorrida pelo carrinho, na situação descrita no texto, tornando a estrada mais lisa.

Resolução

⇒ “Tornar a estrada mais lisa” significa diminuir a intensidade da força de atrito.

⇒ A força de atrito é a força resultante.

⇒ A uma força resultante de menor intensidade corresponde uma aceleração de menor módulo.

⇒ Como o movimento é retardado tal implica, para a mesma velocidade inicial, um maior intervalo de tempo até parar e, em consequência, um maior deslocamento.

⇒ Recorrendo às leis deste movimento, estabelece-se a relação entre a distância percorrida pelo carrinho até parar, v = 0 , e o valor da aceleração.

⇒ Da análise desta expressão e para a mesma velocidade inicial, v₀, verifica-se que quanto menor for o módulo da aceleração maior será a distância percorrida pelo carrinho até parar.

⇒ Tornando a estrada mais lisa, diminuindo o atrito, a distância percorrida pelo carrinho aumenta.

Critérios

A resposta deve apresentar os seguintes tópicos:

A) Quanto mais lisa for a estrada, menor será a intensidade [da resultante] das forças de atrito que atuam sobre o carrinho.

B) Assim, a intensidade da resultante das forças que atuam sobre o carrinho será menor [, uma vez que esta resultante se identifica com a resultante das forças de atrito que atuam sobre o carrinho].

C) Consequentemente, a aceleração do carrinho será menor, pelo que [, para a mesma velocidade inicial,] a distância percorrida pelo carrinho até parar sem maior.

A classificação da resposta a este item é feita em função do enquadramento da mesma num dos níveis de desempenho, de acordo com a tabela seguinte.

11ºano – Física – Domínio 1 – subdomínio 3 (Forças e movimentos)

4. Considere que, movendo-se o carrinho com velocidade aproximadamente constante, uma das rodas dá 5,0 voltas em 4,0 s.

Calcule o valor da velocidade angular dessa roda em radianos por segundo (rad s^-1).

Apresente todas as etapas de resolução.

Resolução

⇒ Para determinar a velocidade angular, ω, tem de se determinar previamente o período, T, do movimento da roda, ou seja, o intervalo de tempo para completar uma volta.

⇒ A velocidade angular da roda é de 2,5 π rad s^-1 ou 7,8 rad s^-1

Critérios

A resolução deve apresentar as seguintes etapas:

A) Determinação do período (T = 0,800 s) OU da frequência (f = 1,25 Hz) do movimento.

B) Determinação do valor da velocidade angular da roda (ω = 7,8 rad s^-1).

A resposta a este item deve ser enquadrada num dos níveis de desempenho relacionados com a consecução das etapas, de acordo com a tabela seguinte.

A classificação a atribuir à resposta resulta da pontuação decorrente do enquadramento num dos níveis de desempenho atrás descritos, à qual podem ser subtraídos pontos, de acordo com o enquadramento nos níveis de desempenho relacionados com o tipo de erros cometidos.

11ºano – Física – Domínio 2 – subdomínio 2 (Eletromagnetismo)

5. Um eixo em rotação pode fazer rodar uma espira condutora numa região do espaço onde exista um campo magnético uniforme, B.

Qual das figuras seguintes representa a situação em que é maior o módulo do fluxo magnético que atravessa a superfície delimitada pela espira?

Resolução

Opção (C)

⇒ Para um campo magnético de determinada intensidade B e para uma certa espira o módulo do fluxo do campo magnético:

| Φ | = B A | cos α|

é máximo quando a normal ao plano da espira e o campo magnético forem paralelos (se α for igual a 0º ou 180º então | cos α | = 1 ), ou seja, quando 1 o plano da espira for perpendicular ao campo magnético.

Critérios

Opção (C)…………. 5 pontos

Grupo II

Com o objetivo de identificar fatores que influenciam a intensidade da força de atrito que atua sobre um corpo que desliza ao longo de um plano inclinado, um grupo de alunos montou uma prancha, com uma certa inclinação em relação à horizontal.

Os alunos realizaram vários ensaios nos quais abandonaram, sobre o plano inclinado, um paralelepípedo de madeira, tendo, em cada ensaio, efetuado as medições necessárias.

10ºano – Física – subdomínio 1 (Energia e movimentos)
A.l. – Medições

1. Em algumas das medições efetuadas, usaram uma fita métrica com uma escala cuja menor divisão é 1 mm.

Qual é a incerteza associada à escala dessa fita métrica?

Resolução

⇒ Os alunos utilizaram um instrumento de medição analógico, pelo que a incerteza associada às medições é igual a metade da sua menor divisão.

⇒ Como no caso da fita métrica utilizada a menor divisão é 1 mm, então a incerteza associada é de ± 0,5 mm.

Critérios

± 0,5 mm ou 0,5 mm (ou equivalente) …………. 5 pontos

10ºano – Física – subdomínio 1 (Energia e movimentos)

2. Numa primeira série de ensaios, os alunos abandonaram o paralelepípedo em diferentes pontos do plano, de modo que aquele percorresse, até ao final do plano, distâncias sucessivamente menores (d₁ > d₂ > d₃ > d₄).

Calcularam, para cada distância percorrida, a energia dissipada e a intensidade da força de atrito que atuou no paralelepípedo.

Os valores calculados encontram-se registados na tabela seguinte.

O que pode concluir-se acerca da relação entre cada uma das grandezas calculadas e a distância percorrida, apenas com base nos resultados registados na tabela?

Resolução

⇒ A energia dissipada aumenta com a distância percorrida.

⇒ A intensidade da força de atrito tem uma variação que apenas é devida à incerteza de medida e, portanto, não depende da distância percorrida.

Critérios

A resposta deve apresentar os seguintes tópicos:

A) A energia dissipada diminui à medida que a distância percorrida sobre o plano diminui.

B) A intensidade da força de atrito é independente da distância percorrida sobre o plano.

A classificação da resposta a este item é feita em função do enquadramento da mesma num dos níveis de desempenho, de acordo com a tabela seguinte.

3. Numa segunda série de ensaios, os alunos colocaram sobrecargas sobre o paralelepípedo e abandonaram esses conjuntos sempre no mesmo ponto do plano.

10ºano – Física – subdomínio 1 (Energia e movimentos)
10ºano – Física – A.l. – 1.1 – Movimento num plano inclinado

3.1. Admita que os alunos abandonaram os conjuntos paralelepípedo + sobrecarga num ponto situado a uma altura de 47,00 cm em relação à base do plano, de modo que esses conjuntos percorressem uma distância de 125,00 cm até ao final do plano, como esquematizado na Figura 1.

Num dos ensaios, usaram um conjunto paralelepípedo + sobrecarga de massa 561,64 g , tendo verificado que este conjunto chegava ao final do plano com uma velocidade de 1,30 ms^-1.

Calcule a intensidade da força de atrito que atuou sobre o conjunto nesse ensaio.

Apresente todas as etapas de resolução.

Resolução

⇒ Trabalho das forças não conservativas:

⇒ O trabalho das forças não conservativas corresponde ao trabalho da força de atrito.

⇒ Admitindo que a força de atrito é constante, calcula-se a intensidade da força de atrito a partir do valor do trabalho desta força:

⇒ Admitindo que a força de atrito é constante o movimento é uniformemente acelerado:

⇒ Intensidade da força de atrito:

Critérios

A resolução deve apresentar as seguintes etapas:

A) Determinação da variação da energia mecânica do sistema considerado (ΔEm = – 2,165 J).

Determinação da intensidade da resultante das forças que atuaram sobre o conjunto (Fr = 0,3797 N).

B) Determinação da intensidade da força de atrito que atuou sobre o conjunto (Fa = 1,73 N).

A resposta a este item deve ser enquadrada num dos níveis de desempenho relacionados com a consecução das etapas, de acordo com a tabela seguinte.

3.2. Os alunos colocaram sobrecargas sobre o paralelepípedo, para averiguar se a intensidade da força de atrito depende

(A) da compressão exercida na rampa pelo conjunto paralelepípedo + sobrecarga.

(B) dos materiais de que são constituídos o plano e o paralelepípedo.

(C) da inclinação da rampa em relação à horizontal.

(D) do coeficiente de atrito cinético do par de materiais em contacto.

*O conteúdo deste item já não faz parte dos atuais referenciais programáticos da disciplina.

Resolução

Opção (A)

⇒ Ao ser colocada a sobrecarga a força de compressão exercida na rampa pelo conjunto paralelepípedo + sobrecarga aumenta.

⇒ Os materiais em contacto e a inclinação permanecem constantes, assim como o coeficiente de atrito cinético (característica dos dois materiais em contacto em movimento relativo).

Critérios

Opção (A)…………. 5 pontos

Grupo III

Considere um sinal sonoro que se propaga no ar.

Na Figura 2, está representada graficamente a pressão do ar, em função do tempo, t , num ponto onde o som foi detetado.

11ºano – Física – Domínio 2 – subdomínio 1 (Sinais e ondas)

1. Por leitura direta do gráfico da Figura 2, é possível obter, relativamente ao som detetado,

(A) o comprimento de onda.

(B) a velocidade de propagação.

(C) o período.

(D) a frequência.

Resolução

Opção (C)

⇒ No gráfico da pressão em função do tempo o que se pode ler diretamente no eixo das abcissas é o tempo, em particular, o intervalo de tempo mínimo de repetição do fenómeno, ou seja, o seu período.

Critérios

Opção (C)…………. 5 pontos

11ºano – Física – Domínio 2 – subdomínio 1 (Sinais e ondas)

2. Se a frequência de vibração da fonte que origina o sinal sonoro aumentasse para o dobro, no mesmo meio de propagação, verificar-se-ia, relativamente ao som detetado, que

(A) o comprimento de onda diminuiria para metade.

(B) o comprimento de onda aumentaria para o dobro.

(C) a velocidade de propagação aumentaria para o dobro.

(D) a velocidade de propagação diminuiria para metade.

Resolução

Opção (A)

⇒ A velocidade de propagação do som, v, é característica do meio portanto mantém-se constante.

⇒ O comprimento de onda, λ, é inversamente proporcional à frequência f.

Critérios

Opção (A)…………. 5 pontos

Grupo IV

O metano, CH₄, é o mais simples dos alcanos, sendo a sua molécula constituída por um átomo de carbono e quatro átomos de hidrogénio.

1. O carbono é um elemento químico formado nas estrelas a partir de reações nucleares. Uma dessas reações envolve a fusão de três núcleos de hélio-4.

Quais devem ser os valores de X e de Y para que o esquema seguinte possa representar a reação de fusão nuclear referida?

3 ⁴₂He → ^X_YC

(A) X = 4 ; Y = 6

(B) X = 12 ; Y = 6

(C) X = 6 ; Y = 12

(D) X = 6 ; Y = 4

*O conteúdo deste item já não faz parte dos atuais referenciais programáticos da disciplina.

Resolução

Opção (B)

⇒ Na reação de fusão deve existir conservação do número de nucleões (protões e neutrões).

Critérios

Opção (B)…………. 5 pontos

2. O átomo de hidrogénio no estado fundamental apresenta um eletrão na orbital 1s .

Do conjunto de números quânticos que descreve aquela orbital, o número quântico principal, n, está relacionado com

(A) a energia da orbital.

(B) a orientação espacial da orbital.

(C) a simetria da orbital.

(D) o número de eletrões na orbital.

*O conteúdo deste item já não faz parte dos atuais referenciais programáticos da disciplina.

Resolução

Opção (A)

⇒ O número quântico principal relaciona-se com a energia da orbital (a simetria está relacionada com o número quântico de momento angular e a orientação espacial com o número quântico magnético).

Critérios

Opção (A)…………. 5 pontos

10ºano – Química – Domínio 2 – subdomínio 1 (Ligação química)

3. A molécula CH₄ apresenta uma geometria tetraédrica.

Indique as posições relativas dos átomos constituintes da molécula CH₄ no tetraedro e refira o tipo de ligações que se estabelecem entre o átomo de carbono e os átomos de hidrogénio.

Resolução

⇒ O átomo de carbono encontra-se no centro do tetraedro e os átomos de hidrogénio nos vértices.

⇒ As ligações entre o átomo de carbono e os átomos de hidrogénio são covalentes simples.

Critérios

A resposta deve apresentar os seguintes tópicos:

A) O átomo de carbono ocupa o centro [do tetraedro], situando-se os quatro átomos de hidrogénio nos vértices do tetraedro.

B) Entre o átomo de carbono e os átomos de hidrogénio estabelecem-se ligações covalentes simples.

A classificação da resposta a este item é feita em função do enquadramento da mesma num dos níveis de desempenho, de acordo com a tabela seguinte.

4. O triclorofluorometano, CFCl₃, é um derivado halogenado do metano.

10ºano – Química – Domínio 2 – subdomínio 1 (Ligação química)

4.1. Selecione a única opção que contém os termos que preenchem, sequencialmente, os espaços seguintes.

Na molécula CFCl₃ ______ pares de eletrões de valência não ligantes, apresentando a molécula um total de _____ pares de electrões de valência ligantes.

(A) existem … oito

(B) existem … quatro

(C) não existem … oito

(D) não existem … quatro

Resolução

Opção (B)

⇒ Na fórmula de estrutura do CFCI₃, representada à direita, apresentam-se os eletrões ligantes, a preto, e os não ligantes, a cinza.

⇒ Portanto, existem eletrões não ligantes e são quatro pares de eletrões ligantes.

Critérios

Opção (B)…………. 5 pontos

10ºano – Química – Domínio 2 – subdomínio 1 (Ligação química)

4.2. A energia média da ligação C-F é 467 kJ mol^-1.

O valor médio da energia, em joule (J), que é libertada quando se estabelece uma ligação C-F é

Resolução

Opção (D)

⇒ E_lig = 467 kJ mol^-1 = 467 x 10³ J mol^-1, pois 1 kJ = 10³ J.

⇒ O valor médio da energia libertada por cada ligação C–F é igual à energia média de ligação por mole (de ligações) a dividir pela constante de Avogadro, N_A (6,02 x 10²³ mol^-1).

Critérios

Opção (D)…………. 5 pontos

10ºano – Química – Domínio 1 – subdomínio 2 (Energia dos eletrões nos átomos)

4.3. Preveja, justificando com base nas configurações eletrónicas de valência dos átomos de flúor (F) e de cloro (Cl) no estado fundamental, em qual desses átomos a remoção de um dos eletrões de valência mais energéticos deverá requerer menor energia.

Resolução

⇒ As configurações eletrónicas dos átomos de flúor e cloro no estado fundamental são:

₉F – 1s² 2s² 2p⁵
₁₇CI – 1s² 2s² 2p⁵ 3s² 3p⁵

⇒ O flúor e o cloro têm o mesmo número de eletrões de valência.

⇒ Os eletrões de valência mais energéticos do átomo de cloro no estado fundamental estão nas orbitais 3p enquanto no estado fundamental do átomo de flúor estão nas orbitais 2p.

⇒ Como o número quântico principal dos eletrões de valência mais energéticos do cloro é maior do que no flúor, os eletrões das orbitais 3p no cloro têm maior energia do que os das orbitais 2p no flúor, sendo, por isso, necessária menos energia para os remover.

⇒ Então, prevê-se que seja necessária menor energia no átomo de cloro para a remoção de um eletrão de valência mais energético.

Critérios

A resposta deve apresentar os seguintes tópicos:

A) Os átomos de flúor e de cloro [, no estado fundamental,] têm configurações eletrónicas de valência semelhantes.

Os elementos flúor e cloro encontram-se no mesmo grupo da Tabela Periódica.

Equivalente.

B) Os eletrões de valência do átomo de cloro encontram-se num nível energético superior ao dos eletrões de valência do átomo de flúor.

C) Prevê-se, assim, que a remoção de um dos eletrões de valência mais energéticos requeira menor energia no átomo de cloro.

A classificação da resposta a este item é feita em função do enquadramento da mesma num dos níveis de desempenho, de acordo com a tabela seguinte.

5. O hidrogénio é produzido industrialmente a partir do metano, segundo uma reação que pode ser representada por

CH₄ (g) + H₂O (g) ⇋ CO (g) + 3 H₂ (g)

11ºano – Química – Domínio 1 – subdomínio 2 (Equilíbrio químico)

5.1. Considere que a constante de equilíbrio, Kc , desta reação é 292, à temperatura T.

Na tabela seguinte, estão registadas as concentrações de equilíbrio, à temperatura T, de três dos gases envolvidos naquela reação.

Calcule a concentração de equilíbrio de monóxido de carbono, CO (g), à temperatura T.

Apresente todas as etapas de resolução.

Resolução

Critérios

A resolução deve apresentar as seguintes etapas:

A) Escrita da expressão que traduz a constante de equilíbrio da reação considerada, sem substituição dos valores conhecidos

Escrita da expressão que traduz a constante de equilíbrio da reação considerada, com substituição dos valores conhecidos

B) Determinação da concentração de equilíbrio de CO (g), à temperatura considerada ([CO] = 4,22 mol dm^-3).

A resposta a este item deve ser enquadrada num dos níveis de desempenho relacionados com a consecução das etapas, de acordo com a tabela seguinte.

11ºano – Química – Domínio 1 – subdomínio 2 (Equilíbrio químico)

5.2. Conclua, justificando, qual é o efeito, na quantidade de H₂ (g), da diminuição da pressão provocada por um aumento do volume do sistema em equilíbrio, admitindo que a temperatura se mantém constante.

Resolução

⇒ De acordo com o Princípio de Le Châtelier, o sistema evolui de modo a contrariar a diminuição de pressão do sistema.

⇒ Para que a pressão aumente é necessário que o sistema evolua no sentido em que aumenta o número de moléculas, ou seja, no sentido da reação direta (por cada 2 moles de reagentes que se consomem formam-se 4 moles de produtos).

⇒ Assim produz-se mais H₂, aumentando a sua quantidade.

⇒ Sempre que a temperatura for constante, a constante de equilíbrio, Kc, mantém-se constante.

⇒ À diminuição de pressão, provocada por um aumento de volume, corresponde uma diminuição das concentrações das espécies de um fator x >1.

⇒ O quociente da reação torna-se menor do que a constante de equilíbrio:

⇒ (o numerador diminui x⁴ vezes e o denominador diminui x² vezes, logo o quociente da reação diminui x⁴/x² = x² vezes).

⇒ Então o sistema químico evoluirá no sentido em que o quociente de reação se aproxime da constante de equilíbrio e, para que isso aconteça, deve aumentar o numerador e diminuir o denominador, ou seja a reação evoluirá no sentido direto.

⇒ Assim, a quantidade de H₂ irá aumentar.

Critérios

A resposta deve apresentar os seguintes tópicos:

A) [De acordo com o Princípio de Le Châtelier,] a diminuição da pressão favorece a reação que conduz a um aumento da pressão OU que conduz a um aumento da quantidade de gases.

B) Neste caso, a reação que conduz a um aumento da pressão (OU a um aumento da quantidade de gases) é a reação direta.

C) Conclui-se, assim, que a quantidade de H₂ (g) irá aumentar.

A classificação da resposta a este item é feita em função do enquadramento da mesma num dos níveis de desempenho, de acordo com a tabela seguinte.

10ºano – Química – Domínio 2 – subdomínio 2 (Gases e dispersões)

6. Considere uma amostra de 8,24 mol de CH₄ (g) e uma amostra de 0,398 mol de CO (g), nas mesmas condições de pressão e de temperatura.

Quantas vezes é que o volume ocupado pela amostra de metano é maior do que o volume ocupado pela amostra de monóxido de carbono?

Apresente o resultado com três algarismos significativos.

Resolução

⇒ Avogadro estabeleceu que, nas mesmas condições de pressão e temperatura, tratando-se de gases ideais (ou gases reais a pressões e temperaturas em que apresentem comportamento de gases ideais), volumes iguais contêm o mesmo número de partículas.

⇒ Nas mesmas condições de pressão e temperatura o volume é diretamente proporcional à quantidade química:

Critérios

20,7 vezes …………. 5 pontos

Nota – O resultado pode ser apresentado com três algarismos significativos numa forma matemática equivalente.

Grupo V

O gás natural, muito utilizado como combustível, é uma mistura cujo principal constituinte é o metano.

10ºano – Química – Domínio 2 – subdomínio 2 (Gases e dispersões)

1. Um dos componentes minoritários que pode existir no gás natural é o azoto, N₂ (g).

A composição em N₂ (g), expressa em partes por milhão em volume, de uma amostra de gás natural que contém 1,3%, em volume, de azoto, pode ser determinada a partir da expressão

Resolução

Opção (A)

⇒ 1,3% em volume significa que existe 1,3 L de N₂ em 100 L de gás natural.

⇒ Num milhão de litros (10⁶) haverá x:

Critérios

Opção (A)…………. 5 pontos

10ºano – Física – subdomínio 3 (Energia, fenómenos térmicos e radiação)

2. Procedeu-se ao aquecimento de 0,800 kg de água, usando como combustível gás natural, que, por cada metro cúbico (m³) consumido, fornece uma energia de 4,0 x 10⁷ J.

A Figura 3 apresenta o gráfico da temperatura dessa amostra de água em função do volume, V, de gás natural consumido.

Determine o rendimento do processo de aquecimento dessa amostra de água.

Apresente todas as etapas de resolução.

c (capacidade térmica mássica da água) = 4,18 x 10³ J kg^-1 ºC^-1

Resolução

⇒ Energia fornecida E para que a temperatura aumente de 22 ºC até 52 ºC (correspondente à
combustão de um volume de 6,0 x 10^-3 m³ de gás natural) :

⇒ Energia absorvida pela água, como calor, para a mesma variação de temperatura:

Q = m c Δθ = 0,800 x 4,18 x 10³ x ( 52 – 22 ) = 1,0 x 10⁵ J

⇒ Determinação do rendimento:

Critérios

A resolução deve apresentar as seguintes etapas:

A) Cálculo da variação de energia interna da água para um certo volume de gás natural consumido.

B) Cálculo da energia fornecida pela combustão do mesmo volume de gás natural.

C) Cálculo do rendimento do processo de aquecimento da amostra de água (η = 42%).

A resposta a este item deve ser enquadrada num dos níveis de desempenho relacionados com a consecução das etapas, de acordo com a tabela seguinte.

10ºano – Física – subdomínio 3 (Energia, fenómenos térmicos e radiação)

3. A Figura 4 representa o esboço do gráfico da temperatura de duas amostras de água, A e B, aquecidas nas mesmas condições, em função da energia que lhes foi fornecida.

Selecione a única opção que contém os termos que preenchem, sequencialmente, os espaços seguintes.

Comparando as ______ das amostras A e B, podemos concluir que a massa da amostra A é _____ à massa da amostra B.

(A) temperaturas finais … superior

(B) temperaturas finais … inferior

(C) variações de temperatura … superior

(D) variações de temperatura … inferior

Resolução

⇒ Para a mesma energia fornecida a cada uma das amostras de água, A e B, verifica-se que Δθ_A é menor do que Δθ_B

⇒ A energia fornecida durante o aquecimento de uma massa de água é:

E = m c Δθ

⇒ m_A c Δθ_A = m_B c Δθ_B ⇔ m_A Δθ_A = m_B Δθ_B

Δθ_A < Δθ_B ⇒ m_A > m_B

⇒ Nas mesmas condições, para a mesma energia fornecida, sofre menor variação de temperatura a que tiver maior massa.

Critérios

Opção (C)…………. 5 pontos

Grupo VI

1. Colocaram-se pequenos pedaços de zinco (Zn) em cada uma de duas soluções aquosas contendo catiões metálicos em concentrações semelhantes: uma solução de sulfato de cobre (II), CuSO₄, e uma solução de nitrato de magnésio, Mg(NO₃)₂.

Os resultados obtidos encontram-se na tabela seguinte.

11ºano – Química – Domínio 2 – subdomínio 2 (Reações de oxidação redução)

1.1. A semi-reação de redução que ocorre pode ser traduzida por

(A) Zn → Zn²⁺ + 2 e^–

(B) Zn²⁺ + 2 e^– → Zn

(C) Cu²⁺ + 2 e^– → Cu

(D) Cu → Cu²⁺ + 2 e^–

Resolução

Opção (C)

⇒ No processo é o cobre que se reduz e o zinco que se oxida.

⇒ O ião cobre reduz-se a cobre metálico.

Critérios

Opção (C)…………. 5 pontos

11ºano – Química – Domínio 2 – subdomínio 2 (Reações de oxidação redução)

1.2. Qual dos três metais (Zn, Cu, Mg) apresenta maior poder redutor?

Resolução

⇒ O zinco tem maior poder redutor do que o cobre, pois oxida-se quando em presença de ião cobre, mas tem menor poder redutor do que o magnésio, porque na presença do ião magnésio não ocorre reação.

Critérios

Magnésio Ou Mg…………. 5 pontos

11ºano – Química – Domínio 2 – subdomínio 2 (Reações de oxidação redução)

2. O ião Cu²⁺ confere à chama uma cor verde azulada, que resulta da sobreposição das radiações

(A) emitidas pelos iões Cu²⁺ em processos de excitação.

(B) emitidas pelos iões Cu²⁺ em processos de desexcitação.

(C) absorvidas pelos iões Cu²⁺ em processos de excitação.

(D) absorvidas pelos iões Cu²⁺ em processos de desexcitação.

Resolução

Opção (B)

⇒ Observa-se luz quando há uma emissão de radiação devida aos processos de desexcitação dos eletrões que estavam em estados excitados.

Critérios

Opção (B)…………. 5 pontos

11ºano – Química – Domínio 1 – subdomínio 1 (Aspetos quantitativos das reações químicas)

3. Uma moeda de cobre de massa 4,10 g foi introduzida numa solução aquosa de nitrato de prata, AgNO₃ (aq).

Ocorreu uma reacção que pode ser traduzida por

Cu (s) + 2 Ag⁺ (aq) → Cu²⁺ (aq) + 2 Ag (s)

Obteve-se 2,65 g de prata sólida.

Calcule a quantidade de cobre que reagiu.

Apresente todas as etapas de resolução.

Resolução

⇒ Quantidade de prata obtida:

⇒ De acordo com a estequiometria da reação para 1 mole de cobre que reage formam-se 2 moles de prata, logo a quantidade de cobre que reagiu é metade da quantidade de prata que se obteve:

Critérios

A resolução deve apresentar as seguintes etapas:

A) Determinação da quantidade de prata obtida (n = 2,457 x 10^-2 mol).

B) Determinação da quantidade de cobre que reagiu (n = 1,23 x 10^-2 mol).

A resposta a este item deve ser enquadrada num dos níveis de desempenho relacionados com a consecução das etapas, de acordo com a tabela seguinte.

11ºano – Química – Domínio 2 – subdomínio 3 (Soluções e equilíbrio de solubilidade)

4. O cloreto de prata, AgCl, é um sal cujo produto de solubilidade é, a 25 ºC, 1,8 x 10^-10.

Numa solução aquosa contendo iões Ag⁺ e Cl^–, a 25 ºC, formar-se-á um precipitado de AgCl, se

(A) as concentrações daqueles iões forem inferiores à solubilidade do AgCl.

(B) as concentrações daqueles iões forem iguais à solubilidade do AgCl.

(C) o produto das concentrações daqueles iões for superior a 1,8 x 10^-10.

(D) o produto das concentrações daqueles iões for inferior a 1,8 x 10^-10.

Resolução

Opção (C)

⇒ O produto de solubilidade do cloreto de prata é:

Ks = |Ag⁺|_e |Cl^–|_e

⇒ A solubilidade é igual à concentração do cloreto de prata no equilíbrio.

⇒ Se o produto da concentração dos iões prata pela concentração dos iões cloreto for maior do que Ks ocorre formação de sólido (precipitado).

Critérios

Opção (C)…………. 5 pontos

FIM

2011 – 1ª Fase – Prova Escrita de Física e Química A

Deixe um comentário Cancelar resposta

1468

2053

198

10

Receba novidades

Cursos

Links úteis

Utilizador