2020 – 1ªFase – Prova Escrita de FQ A
Voltar a: Física e Química
- Prova Escrita de Física e Química A – versão 1
- Prova 715: 1.ª Fase – 2020
Nota: A prova inclui 8 itens, devidamente identificados no enunciado, cujas respostas contribuem obrigatoriamente para a classificação final (itens I ‒ 2.1., I ‒ 3.1., I ‒ 3.2.1., II ‒ 1.3.1., II ‒ 2., III ‒ 3., IV ‒ 2. e IV ‒ 5.2.).
Dos restantes 18 itens da prova, apenas contribuem para a classificação final os 12 itens cujas respostas obtenham melhor pontuação.
GRUPO I
Recriando uma das famosas experiências realizadas por Galileu, estudou-se o movimento de translação de uma esfera largada sobre um plano inclinado.
Considere que a esfera pode ser representada pelo seu centro de massa (modelo da partícula material).
Admita que, em cada ensaio realizado, o módulo da velocidade da esfera aumentou proporcionalmente com o tempo decorrido e que a resultante das forças de atrito que atuaram na esfera não foi desprezável.
- 11ºano – Física – Domínio 1 – subdomínio 2 (Interações e os seus efeitos)
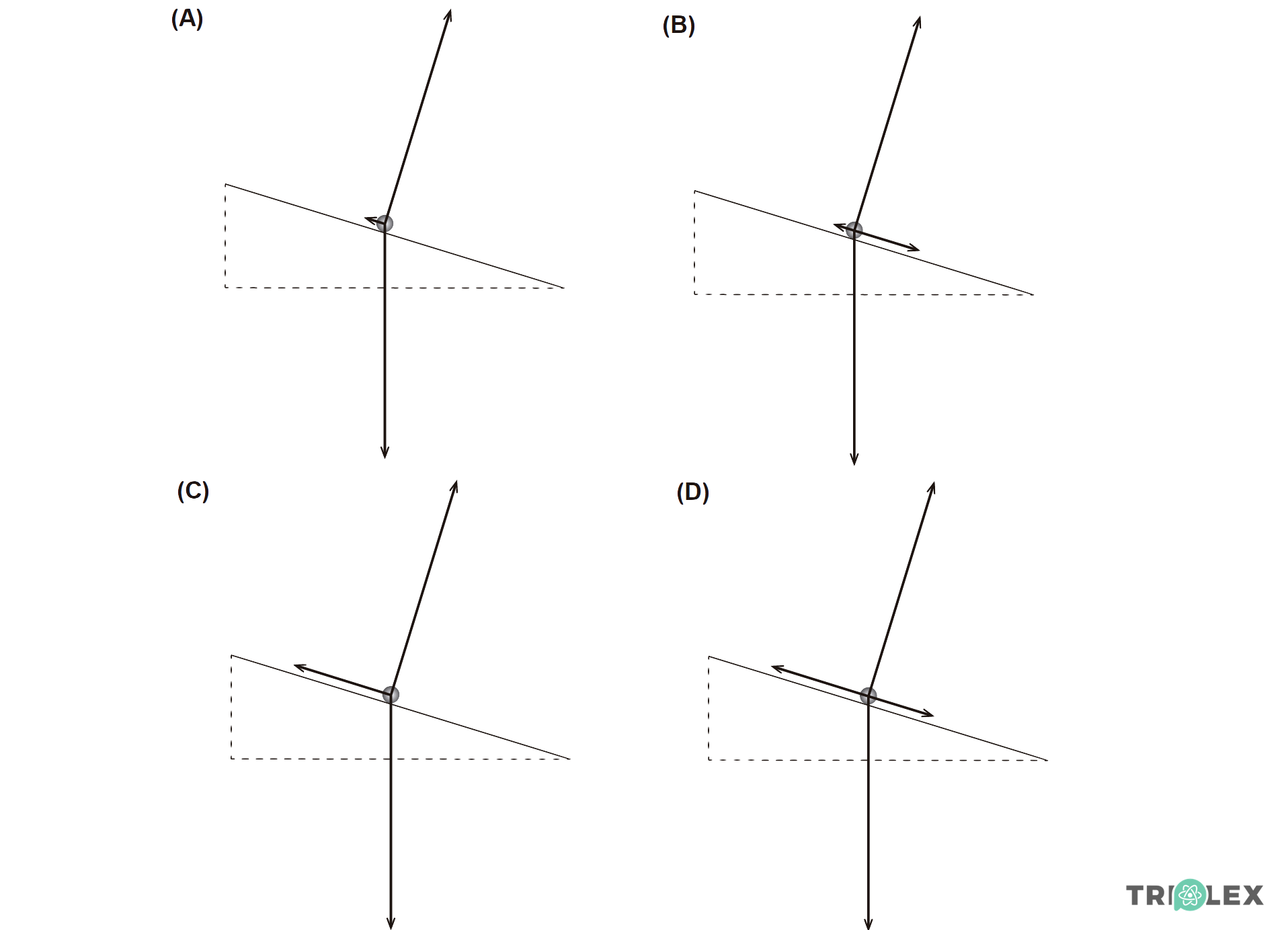
1. Qual dos diagramas pode representar, na mesma escala, as forças que atuam na esfera durante a descida no plano inclinado?
- Opção (A)
⇒ Na esfera atuam a força gravítica (vertical), a força normal (perpendicular ao plano inclinado) e a força de atrito (paralela ao plano inclinado).
⇒ Como a velocidade da esfera aumenta, a resultante das forças tem o sentido do movimento, logo a força de atrito é menor do que a componente da força gravítica na direção do plano inclinado.
- Opção (A) ……………. 10 pontos
2. Na recriação da experiência de Galileu, foi utilizado um plano inclinado, de comprimento L, que está esquematizado na Figura 1.
Em dois dos ensaios realizados, a esfera foi largada de duas posições diferentes, A e B, tendo-se medido o tempo que a esfera demorou a atingir a posição C.

- 10ºano – Física – subdomínio 1 (Energia e movimentos)
2.1 O trabalho realizado pela força gravítica que atua na esfera, desde a posição de onde é largada até à posição C, da posição inicial da intensidade da resultante das forças de atrito que atuam na esfera.
(A) depende … e depende
(B) depende … e não depende
(C) não depende … e depende
(D) não depende … e não depende
A pontuação obtida na resposta contribui obrigatoriamente para a classificação final da prova.
- Opção (B)
⇒ Num dado local, o trabalho realizado pela força gravítica, WFg, depende da massa, m, da esfera e da variação de altura, Δℎ:
- WFg = −ΔEpg = −mg Δℎ = mg (ℎi − ℎf)
portanto, para uma dada esfera (m constante) e para a mesma posição final (mesmo ℎf) dependerá apenas da altura da posição inicial, ℎi.
- Opção (B) ……………. 10 pontos
- 11ºano – Física – Domínio 1 – subdomínio 3 (Forças e movimentos)
2.2 Considere que tA e tB são os tempos que a esfera demora a atingir a posição C quando é largada das posições A e B, respetivamente.
Determine o quociente desses tempos.
Mostre como chegou ao valor solicitado.
⇒ Em cada ensaio realizado, o módulo da velocidade da esfera aumentou proporcionalmente com o decorrido, ou seja, a aceleração foi constante.
⇒ Dado que as condições experimentais se mantiveram (a mesma esfera foi largada sobre um plano inclinado), a aceleração, de módulo a, foi necessariamente a mesma em todos os ensaios.
⇒ Como a esfera é largada, a velocidade inicial é nula em ambos os casos.
⇒ A distância percorrida é dada pela expressão:
- x = x0 + v0t + ½ at2
⇒ Teremos:
- xA = L = ½ at2A
- xB = L – L/4 = ½ at2B
⇒ Usando a expressão de L da primeira equação e substituindo na segunda, obtém-se:
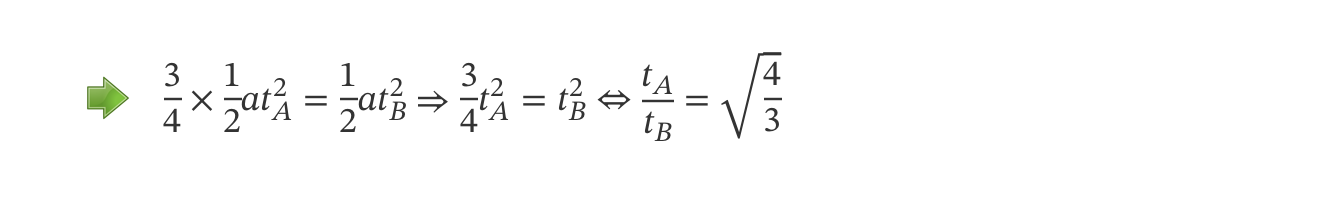
3. Os tempos de descida da esfera sobre o plano inclinado foram medidos indiretamente a partir dos volumes de água vertidos por uma bureta.
Assim, em cada ensaio realizado, abriu-se a torneira da bureta no instante em que a esfera foi largada sobre o plano inclinado e fechou-se a torneira da bureta no instante em que a esfera atingiu a base do plano.
- 10ºano – Química – Domínio 1 – subdomínio 1 (Massa e tamanho dos átomos)
- 10ºano – Química – A.l. – 1.1 – Volume e número de moléculas numa gota de água
3.1 Na Figura 2, reproduzem-se duas fotografias (I e II) de parte da bureta, graduada em cm3, nas quais se observa o nível da água no início (I) e no final (II) de um dos ensaios.

Qual foi o volume de água escoado nesse ensaio?
Apresente o valor solicitado com o número correto de algarismos significativos.
A pontuação obtida na resposta contribui obrigatoriamente para a classificação final da prova.
- O volume de água escoado foi 4,40 cm3
⇒ O volume de água escoado é a diferença entre o nível de água no final (6,00 cm3) e o nível de água no início (1,60 cm3).
- Apresenta o valor solicitado (4,40 cm3) ……………. 10 pontos
3.2 Considere que, nos ensaios realizados, a bureta vertia, aproximadamente, 1,6 cm3 de água em cada segundo.
A massa volúmica da água, nas condições em que foram realizados esses ensaios, é 1,0 g cm-3.
- 10ºano – Química – Domínio 1 – subdomínio 1 (Massa e tamanho dos átomos)
- 10ºano – Química – A.l. – 1.1 – Volume e número de moléculas numa gota de água
3.2.1 Quantas moléculas de água foram, aproximadamente, vertidas pela bureta em cada segundo?
(A) 6,8 x 1024
(B) 9,6 x 1023
(C) 3,8 x 1023
(D) 5,3 x 1022
A pontuação obtida na resposta contribui obrigatoriamente para a classificação final da prova.
- Opção (D) ……………. 10 pontos
- 11ºano – Física – Domínio 1 – subdomínio 3 (Forças e movimentos)
- 11ºano – Física – A.l. – 1.3 – Movimento uniformemente retardado
3.2.2 Na tabela seguinte, estão registadas as distâncias, d, percorridas pela esfera, largada de diferentes posições sobre o plano inclinado, e os volumes, V, de água vertidos até a esfera atingir a base do plano.

Determine o módulo da aceleração da esfera, em m s-2, a partir da equação da reta de ajuste a um gráfico adequado.
Na resposta:
– apresente uma tabela com os valores a utilizar na construção do gráfico, identificando as variáveis consideradas;
– apresente a equação da reta de ajuste a esse gráfico;
– calcule o valor solicitado.
Explicite o seu raciocínio, indicando todos os cálculos efetuados.
⇒ O volume, V, vertido pela bureta num intervalo de tempo t é V = 1,6t (V em cm3 e em s).
⇒ Num movimento retilíneo em que a velocidade aumenta proporcionalmente com o tempo, a distância percorrida é:
- x = x0 + v0t + ½ at2 ⇔ d = ½ at2
Sendo a esfera largada, a velocidade inicial é nula ( v = 0).
⇒ Das relações anteriores obtém-se
- d em m e V em cm3
⇒ d varia linearmente com V2 (V é uma medida do tempo).
- Os valores a utilizar na construção do gráfico d = f(V2) são apresentados na tabela.
⇒ A equação da reta de ajuste ao gráfico é d = 9,583 x 10-2 V2 + 0,035.
A ordenada na origem resulta de incertezas experimentais, podendo concluir-se que
- a/5,12 = 9,583 x 10-2 m s-2 ⟺ a = 0,49 m s-2.
ou
⇒ O movimento da esfera sobre o plano inclinado é relativo e uniformemente acelerado, descrito pela equação:
- x = x0 + v0t + ½ at2 ⇔ d = ½ at2
donde d = x – x0 é a distância percorrida e v0 = 0 ( a esfera é largada).
⇒ Representado d em função de t2, deve obter-se uma reta de ajuste aos pontos do gráfico.
⇒ O módulo do declive desta reta corresponde a metade do módulo da aceleração da esfera.
O tempo t que a esfera demora a atingir a base do plano é dado por t = V/1,6, em que V é o volume de água vertido em cada ensaio, e 1,6 cm3 s-1 é o volume de água vertido por segundo.
⇒ A tabela seguinte tem na primeira coluna as distâncias d (em m) percorridas pela esfera e na segunda os valores correspondentes de t2 ( em s2).
⇒ A equação da reta de ajuste aos pontos do gráfico d (t2) = 0,244 t2 + 4 x 10-2
⇒ Obtém-se o módulo da aceleração da esfera, a, a partir da relação
- 0,244 ms-2 = ½ a ⇔ a = 0,49 ms-2
- Determina o valor solicitado, percorrendo as etapas seguintes:
⇒ Calcula o tempo de escoamento, t , correspondente a cada volume de água vertido …….. 2 pontos
⇒ Apresenta uma tabela com os valores de d e de t2 a utilizar na construção do gráfico …….. 3 pontos
⇒ Apresenta a equação da reta de ajuste ao gráfico t2 = f(d) ou ao gráfico d = f(t2) (t2 = 4,09d – 0,2 ou d = 0,244 t2 + 4 x 10-2) (ver nota) …….. 2 pontos
⇒ Calcula o módulo da aceleração da esfera (a = 0,49 m s-2 ) …….. 3 pontos
ou
⇒ Apresenta uma tabela com os valores de d e de V2 a utilizar na construção do gráfico …….. 2 pontos
⇒ Apresenta a equação da reta de ajuste ao gráfico V2 = f(d) ou ao gráfico d = f (V2) ( V2 = 10,41 d – 0,31 ou d = 9,583 x 10-2 V2 + 4 x 10-2) (ver nota) …….. 2 pontos
⇒ Utiliza a relação entre o volume e o tempo de escoamento para obter uma expressão de t2 = f(d) (t2 = 4,07 d) ou para obter uma expressão de d = f (t2) (d = 0,245 t2) ou para obter, a partir da equação das posições, uma expressão que relacione d com V2 (d = ½ a V2/1,62 ou equivalente) …….. 3 pontos
⇒ Calcula o módulo da aceleração da esfera (a = 0,49 m s-2 ) …….. 3 pontos
Nota :
- A omissão da ordenada na origem não implica qualquer desvalorização.
GRUPO II
1. Na Figura 3, apresentam-se os gráficos do módulo da velocidade, v, de duas gotas de água, A e B, de diferentes diâmetros, em queda vertical, em função da distância, d, percorrida pelas gotas.
Considere que as gotas de água podem ser representadas pelo seu centro de massa (modelo da partícula material).

- 11ºano – Física – Domínio 1 – subdomínio 3 (Forças e movimentos)
1.1 Considere o deslocamento total de 2,0 m da gota A.
Sejam Fg e Far as forças gravítica e de resistência do ar, respetivamente, que atuam na gota A.
O trabalho realizado por Fg é variação da energia potencial gravítica do sistema gota A + Terra e é, em módulo, do que o trabalho realizado por Far .
(A) simétrico da … menor
(B) igual à … menor
(C) simétrico da … maior
(D) igual à … maior
- Opção (C)
⇒ O trabalho realizado por Fg é simétrico da variação da energia potencial gravítica do sistema gota A + Terra (WFg = −ΔEpg)
⇒ A soma dos trabalhos realizados por Fg e por Far é positiva, dado que a energia cinética de A aumenta:
- WFg + WFar = ΔEc > 0
⇒ Como WFg é positivo (Fg tem o sentido do movimento) e WFar é negativo (Far tem sentido oposto ao do movimento) conclui-se que, em módulo, é maior do que
- WFg + WFar > 0 ⇔ WFg > – WFar ⇔ |WFg | > |WFar |
- Opção (C) ……………. 10 pontos
- 11ºano – Física – Domínio 1 – subdomínio 3 (Forças e movimentos)
1.2 Conclua se a intensidade da resultante das forças que atuam na gota A é maior nos primeiros 0,1 m ou nos últimos 0,1 m da queda a que se refere o gráfico da Figura 3.
Mostre como chegou à conclusão solicitada.
⇒ As forças que atuam sobre a gota são a força gravítica, Fg, com a direção e sentido do movimento e cuja intensidade se mantém constante durante todo o percurso, e a força de resistência do ar, Far, com a direção do movimento, sentido oposto e intensidade variável.
⇒ No primeiro percurso de 0,1 m, a gota A parte do repouso e o módulo da sua velocidade aumenta sempre: o movimento da gota é acelerado, a força resultante tem a direção e sentido do movimento (a intensidade de Far mantém-se sempre inferior à intensidade de Fg).
⇒ No último percurso de queda de 0,1 m, a velocidad da gota mantém-se constante: o movimento é retilíneo e uniforme, a aceleração é nula e força resultante também é nula ( a intensidade der Far é igual à intensidade de Fg).
⇒ Assim, conclui-se que a intensidade da resultante das forças que atuam na gota A é maior nos primeiros 0,1 m do seu percurso.
1.3 A massa da gota B é 4,2 x 10-3 g.
- 10ºano – Física – subdomínio 1 (Energia e movimentos)
1.3.1 Determine a energia dissipada na queda de 2,0 m da gota B.
Explicite o seu raciocínio, indicando todos os cálculos efetuados.
A pontuação obtida na resposta contribui obrigatoriamente para a classificação final da prova.
⇒ O trabalho que seria realizado pela resultante das forças de resistência do ar (resultante das forças não conservativas) é igual à variação de energia mecânica do sistema gota B + Terra na queda de 2,0 m:
- WFar = ΔEm = ΔEc + ΔEc = (½ mvi2 – 0 ) + mg Δh
- WFar = ½ x 4,2 x 10-6 x 5,02 + 4,2 x 10-6 x 10 x (-2,0) = 3,2 x 10-5 J
- Determina o valor solicitado, percorrendo as etapas seguintes:
⇒ Calcula a variação da energia potencial gravítica do sistema gota B + Terra (ΔEp = -8,40 x 10-5 J) …….. 3 pontos
⇒ Calcula a variação da energia cinética da gota B ( ΔEc = 5,25 x 10-5 J) …….. 3 pontos
⇒ Calcula a energia dissipada na queda de 2,0 m da gota B (E = 3,2 x 10-5 J) (ver nota) …….. 4 pontos
Nota ‒ A apresentação do valor «-3,2 x 10-5 J» não implica qualquer desvalorização.
- 10ºano – Física – subdomínio 3 (Energia, fenómenos térmicos e radiação)
1.3.2 Considere que, em determinadas condições, a variação de entalpia (mássica) de vaporização da água é 2,4 kJ g-1 .
A energia necessária para a vaporização da gota B, nessas condições, é
(A) 0,57 J
(B) 10 J
(C) 0,57 kJ
(D) 10 kJ
- Opção (B)
⇒ A energia necessária para a vaporização da gota, Evap, depende da massa m da gota e da variação mássica de vaporização, Δhvap:
- Evap =m Δhvap = 4,2 x 10-3 x 2,4 x 103 = 10 J
- Opção (B) ……………. 10 pontos
- 10ºano – Física – subdomínio 3 (Energia, fenómenos térmicos e radiação)
2. Considere que foi fornecida, à pressão de 1 atm, a mesma energia a uma gota de água e a uma amostra de ar com o dobro da massa dessa gota.
A essa pressão, a capacidade térmica mássica da água líquida é cerca de quatro vezes superior à capacidade térmica mássica do ar.
A variação de temperatura da gota, comparada com a variação de temperatura da amostra de ar, será, aproximadamente,
(A) oito vezes maior.
(B) oito vezes menor.
(C) duas vezes maior.
(D) duas vezes menor.
A pontuação obtida na resposta contribui obrigatoriamente para a classificação final da prova.
- Opção (D)
⇒ A variação de temperatura, ΔT, de um sistema de massa m e capacidade térmica mássica c relaciona-se com a energia, E, recebida pelo sistema através da expressão E = mcΔT.
⇒ Como a energia fornecida à gota de água e à amostra de ar foram iguais, teremos:
- mágua cágua ΔTágua = mar car ΔTar
⇒ Relacionando as massas e as capacidades térmicas da água e do ar:
- mágua cágua ΔTágua = 2 x mágua x (1/4) x cágua ΔTágua ⇔ ΔTágua = ½ ΔTar
- Opção (D) ……………. 10 pontos
GRUPO III
1. Uma espira circular na proximidade de um íman fixo roda num mesmo plano horizontal, em torno de um eixo vertical, z, que passa pelo centro da espira, C, como se esquematiza na Figura 4.

- 11ºano – Física – Domínio 2 – subdomínio 2 (Eletromagnetismo)
1.1 Na situação descrita, o fluxo magnético através da superfície plana delimitada pela espira, e a força eletromotriz induzida na espira nula.
(A) varia … é
(B) varia … não é
(C) não varia … é
(D) não varia … não é
- Opção (C)
⇒ A rotação da espira não altera o campo magnético em pontos da superfície delimitada pela espira (a posição da espira relativamente ao íman mantém-se), logo o fluxo magnético através dessa superfície mantém-se constante, ΔΦm = 0.
⇒ Conclui- se que a força eletromotriz induzida na espira é nula:
- Opção (C) ……………. 10 pontos
- 11ºano – Física – Domínio 2 – subdomínio 2 (Eletromagnetismo)
1.2 Os pontos A e C pertencem à mesma linha de campo magnético.
Nas figuras seguintes, está representado o campo magnético criado pelo íman no ponto A, BA.
Em qual das figuras pode estar representado o campo magnético criado pelo íman no ponto C, BC?

- Opção (B)
⇒ A densidade de linhas do campo magnético criado pelo íman diminui com o aumento da distância ao íman.
⇒ Como a intensidade do campo é proporcional à densidade de linhas de campo, conclui-se que o campo no ponto C, BC, é menos intenso do que o campo no ponto A, BA.
- Opção (B) ……………. 10 pontos
- 11ºano – Física – Domínio 2 – subdomínio 2 (Eletromagnetismo)
2. Uma corrente elétrica é induzida numa bobina quando uma antena recebe um sinal eletromagnético de 800 kHz, emitido por uma estação de rádio.
Qual é o comprimento de onda, no ar, da onda associada à propagação daquele sinal?
(A) 3,75 x 105 km
(B) 3,75 x 102 m
(C) 2,67 x 10-6 km
(D) 2,67 x 10-9 m
- Opção (B) ……………. 10 pontos
- 10ºano – Física – subdomínio 2 (Energia e fenómenos elétricos)
3. Na Figura 5, está representado um circuito elétrico com:
• um gerador de força eletromotriz 9,20 V e resistência interna 2,0 Ω ;
• um voltímetro ligado nos terminais do gerador;
• dois condutores, A e B, de resistências elétricas RA e RB , sendo RA = 3 RB.
Determine a potência dissipada no condutor A quando o voltímetro marca 8,74 V.
Explicite o seu raciocínio, indicando todos os cálculos efetuados.
A pontuação obtida na resposta contribui obrigatoriamente para a classificação final da prova.
⇒ A corrente elétrica, I, fornecida pelo gerador, obtém-se a partir da expressão U = ε – rI, que relaciona a diferença de potencial elétrico, U, nos terminais do gerador, com a sua força eletromotriz ε e a sua residência interna, r.
⇒ Usando os dados, temos:
- 8,74 V = 9,20 V – 2,0 Ω x I ⇒ I = 0,230 A
⇒ As diferenças de potencial elétrico nos terminais dos condutores são iguais:
- UA = UB
⇒ A resistência do condutor A é triplo da do condutor B:
- RA = 3 RB
⇒ Por outro lado, verifica-se que I = IA + IB, onde IA e IB designam as correntes elétricas nos condutores A e B, respetivamente.
⇒ Usando as relações anteriores, temos:
⇒ A resistência do condutor A, RA, calcula-se a partir de:
- UA = RA x IA ⇒ 8,74 = RA x 0,0575 ⇒ RA = 152 Ω
⇒ A potência dissipada no condutor A é:
- Pdiss,A = RA IA2 = 152 x (0,0575)2 = 0,50 W
ou
⇒ Como a potência dissipada no condutor é igual à potência elétrica que recebe do gerador, pode obter-se o mesmo resultado, a partir de:
- Pdiss,A = UA IA = 8,74 x 0,0575 = 0,50 W
- Determina o valor solicitado, percorrendo as etapas seguintes:
⇒ Calcula a corrente elétrica fornecida pelo gerador (I = 0,230 A) …….. 3 pontos
⇒ Calcula a corrente elétrica que percorre o condutor A ( IA = 5,75 x 10-2 A)
ou
- Obtém uma expressão que relaciona a potência dissipada no condutor A com a potência fornecida pelo gerador ( 4 PA = PG) …….. 4 pontos
⇒ Calcula a potência dissipada no condutor A (PA = 0,50 W) …….. 3 pontos
GRUPO IV
A concentração de dióxido de carbono, CO2, na atmosfera terrestre tem aumentado de forma muito significativa desde meados do século XIX.
Para esse aumento têm contribuído, entre outros fatores, a crescente utilização de combustíveis fósseis e a desflorestação.
- 10ºano – Química – Domínio 1 – subdomínio 1 (Massa e tamanho dos átomos)
1. Na natureza, existem três isótopos de carbono: 12C , 13C e 14C.
Átomos destes isótopos têm o mesmo número de
(A) protões e massas diferentes.
(B) protões e massas iguais.
(C) neutrões e massas iguais.
(D) neutrões e massas diferentes.
- Opção (A)
⇒ Isótopos são átomos do mesmo elemento, ou seja, com o mesmo número de protões, e que diferem no número de neutrões e, consequentemente, na massa.
- Opção (A) ……………. 10 pontos
- 10ºano – Química – Domínio 1 – subdomínio 3 (Tabela periódica)
2. Compare o átomo de oxigénio com o átomo de carbono, ambos no estado fundamental.
Os eletrões de valência do átomo de oxigénio são, em média, atraídos pelo núcleo, tendo este átomo raio atómico.
(A) mais … maior
(B) menos … maior
(C) mais … menor
(D) menos … menor
A pontuação obtida na resposta contribui obrigatoriamente para a classificação final da prova.
- Opção (C)
⇒ 6C – 1s2 2s2 2p2 ;
⇒ 8O – 1s2 2s2 2p4;
Os eletrões de valência dos átomos de carbono e de oxigénio no estado fundamental encontram-se no mesmo nível de energia (n = 2).
⇒ A carga nuclear do átomo de oxigénio (+8) é superior à do átomo de carbono (+6), por isso, sobre os eletrões de valência é mais intensa a força atrativa exercida pelo núcleo do átomo de oxigénio do que a exercida pelo núcleo do átomo de carbono.
- Em consequência, o raio atómico do oxigénio é menor do que o raio atómico do carbono.
- Opção (C) ……………. 10 pontos
- 10ºano – Química – Domínio 2 – subdomínio 1 (Ligação química)
3. A molécula de CO2 apresenta eletrões de valência ligantes e eletrões de valência não ligantes.
(A) quatro … quatro
(B) quatro … oito
(C) oito … quatro
(D) oito … oito
- Opção (D)
⇒ Na molécula de CO2 existem, no total, dezasseis eletrões de valência (quatro que provêm do átomo de carbono e seis de cada um dos dois átomos de oxigénio).
⇒ Desses eletrões de valência, oito são eletrões ligantes partilhados pelo átomo de carbono e pelos átomos de oxigénio em duas ligações duplas.
⇒ Os restantes oito eletrões de valência são não ligantes.
- Opção (D) ……………. 10 pontos
4. A combustão do metano, CH4 (g), pode ser traduzida por
CH4 (g) + 2 O2 (g) → CO2 (g) + 2 H2O (g)
- 11ºano – Química – Domínio 2 – subdomínio 2 (Reações de oxidação redução)
4.1 Qual é a variação do número de oxidação do carbono na reação considerada?
(A) +8
(B) -8
(C) +4
(D) -4
- Opção (A)
⇒ O número de oxidação do carbono é −4 no reagente CH4 (g) e +4 no produto CO2 (g), pelo que a variação do número de oxidação do carbono na reação considerada é +8 (Δ n. o. (C) = (+4 – (−4)).
- Opção (A) ……………. 10 pontos
- 11ºano – Química – Domínio 1 – subdomínio 1 (Aspetos quantitativos das reações químicas)
4.2 Em muitas reações de combustão, que ocorrem em sistemas reais, o combustível não reage completamente, mesmo existindo O2 (g) em excesso.
Considere que, numa reação de combustão de metano, por cada mole de CH4 (g), 0,016 mol não reagiram, apesar de existir um excesso de 5,0% de O2 (g).
Admita que, além da reação considerada, não ocorrem outras reações.
Determine, por cada mole de CH4 (g), a quantidade de O2 (g) que não reagiu.
Explicite o seu raciocínio, indicando todos os cálculos efetuados.
⇒ Da estequiometria da reação de combustão considerada (1 mol de CH4 para 2 mol de O2), deduz-se que, por cada mole de CH4 (g), a quantidade de O2 (g) introduzida em excesso (5,0%) é 0,050 x 2 mol = 0,100 mol.
⇒ Analogamente, a quantidade de O2 (g) que reagiria com 0,016 mol de CH4 (g) ( o que não reage por cada mole de CH4 (g) seria 2 x 0,016 mol = 0,032 mol
⇒ Assim, por cada mole de CH4 (g), a quantidade de O2 (g) que não reagiu foi :
- (0,100 + 0,032) mol ≈ 0,13 mol
ou
⇒ Cálculo da quantidade de O2 (g) disponível, por cada mole de CH4 (g):
De acordo com estequiometria da reação, com 1 mol CH4 reagem 2 mol O2.
⇒ Cálculo da quantidade de O2 (g) que reagiu, por cada mole de CH4 (g)
- CH4 que reagiu = 1 mol − 0,016 mol = 0,984 mol
⇒ Cálculo da quantidade de O2 (g) que não reagiu, por cada mole de CH4 (g)
- n(O2 não reagiu ) = n(O2 disponível ) – n(O2 reagiu ) = (2,100 – 1,968) mol = 0,13 mol
- Determina o valor solicitado, percorrendo as etapas seguintes:
⇒ Calcula, por cada mole de CH4 (g), a quantidade de O2 (g) disponível (n = 0,100 mol) …….. 3 pontos
⇒ Calcula, por cada mole de CH4 (g), a quantidade de O2 (g) que reagiu (n = 0,032 mol) …….. 2 pontos
⇒ Calcula, por cada mole de CH4 (g), a quantidade de O2 (g) que não reagiu (n = 0,13 mol) …….. 5 pontos
ou
⇒ Calcula, por cada mole de CH4 (g), a quantidade de O2 (g) introduzida em excesso (n = 0,100 mol) …….. 3 pontos
⇒ Calcula a quantidade de O2 (g) que deveria ter reagido com 0,016 mol de CH4 (g) (n = 0,032 mol) …….. 2 pontos
⇒ Calcula, por cada mole de CH4 (g), a quantidade de O2 (g) que não reagiu (n = 0,13 mol) …….. 5 pontos
5. A curva de Keeling, obtida a partir de medidas rigorosas efetuadas no observatório de Mauna Loa, no Havai, evidencia o aumento da concentração de CO2 na troposfera, nas últimas décadas.
A curva de Keeling representada na Figura 6 traduz a fração molar média de CO2 , XCO2 , em amostras de ar seco, em função do tempo, t, em anos, a, entre 1958 e 2018.

- 10ºano – Química – Domínio 2 – subdomínio 2 (Gases e dispersões)
5.1 Qual foi o teor médio de CO2 nas amostras recolhidas em 1965, em partes por milhão em volume?
(A) 3,20 x 10-4 ppm
(B) 3,20 x 102 ppm
(C) 3,20 x 10-2 ppm
(D) 3,20 x 106 ppm
- Opção (B)
⇒ A fração molar média de CO2 nas amostras recolhidas em 1965 é 3,20 x 10-4, o que significa que, nesse ano, existiam 3,20 x 10-4 mol de CO2 por cada mole de moléculas no ar.
⇒ Como, nas mesmas condições de pressão e de temperatura, o volume d um gás (ideal) é diretamente proporcional ao numero de moléculas, o quociente do volume de CO2 pelo volume de ar é igual à fração molar de CO2:
 ⇒ Conclui-se que o teor médio de CO2 nas amostras recolhidas em 1965 é 3,2 x 102 partes por milhão.
⇒ Conclui-se que o teor médio de CO2 nas amostras recolhidas em 1965 é 3,2 x 102 partes por milhão.
ou

- Opção (B) ……………. 10 pontos
- 10ºano – Química – Domínio 2 – subdomínio 2 (Gases e dispersões)
5.2 Determine, a partir da curva de Keeling representada na Figura 6, a taxa temporal média, entre 1999 e 2015, de variação da massa de CO2 por dm3 de ar seco (medido em condições PTN), em g dm-3 a-1.
Explicite o seu raciocínio, indicando todos os cálculos efetuados.
A pontuação obtida na resposta contribui obrigatoriamente para a classificação final da prova.
⇒ Por leitura do gráfico, as frações molares médias de CO2 em 1999 e em 2015 são, respetivamente,
- X(CO2) 1999 = 3,68 x 10-4
- X(CO2) 2015 = 4,00 x 10-4
ou
⇒ Por leitura do gráfico, as frações molares médias de CO2 em 1999 e em 2015 são, respetivamente,
- X(CO2) 1999 = 3,68 x 10-4
- X(CO2) 2015 = 4,00 x 10-4
⇒ Cálculo da quantidade de matéria de CO2 em 1999 e em 2015 em 1 dm3 de ar seco
⇒ Cálculo da massa de CO2 em 1999 e em 2015 em 1 dm3 de ar seco
⇒ Cálculo da taxa temporal média, entre 1999 e 2015, de variação da massa de CO2 por dm3 de ar seco

- Determina o valor solicitado (3,9 x 10-6 d dm-3 a-1) (ver nota 1), percorrendo as etapas seguintes (ver nota 2):
⇒ Indica a fração molar média de CO2 em 1999 e em 2015 (3,68 x 10-4 e 4,00 x 10-4) …….. 1 pontos
⇒ Utiliza o conceito de volume molar para calcular, pelo menos, uma quantidade (ou uma massa) de CO2 por dm3 de ar seco …….. 4 pontos
⇒ Utiliza o conceito de massa molar para calcular, pelo menos, uma massa de CO2 …….. 2 pontos
⇒ Calcula uma taxa temporal média, entre 1999 e 2015 …….. 3 pontos
Notas:
1. A ausência de unidade no valor solicitado não implica qualquer desvalorização.
2. Com exceção das leituras no gráfico, as restantes etapas podem ser percorridas por qualquer ordem.
- 11ºano – Química – Domínio 1 – subdomínio 2 (Equilíbrio químico)
2 CO (g) + O2 (g) ⇋ 2 CO2 (g) Kc = 2 x 1022 , a 1000 K
A ordem de grandeza da constante de equilíbrio, Kc, à temperatura considerada, indica que(A) a formação dos produtos da reação é favorecida.
(B) o produto da reação se forma muito rapidamente.
(C) a reação tem rendimento muito elevado.
(D) ambos os reagentes se esgotam.
- Opção (A)
⇒ Um constante de equilíbrio, Kc, muito elevada implica que, num qualquer estado de equilíbrio, o produto das concentrações dos produtos é muito maior do que o produto das concentrações dos reagentes (elevados aos respetivos coeficientes estequiométricos), traduzindo o favorecimento da reação de formação dos produtos.
⇒ A velocidade da reação de formação dos produtos depende de diversos fatores como, por exemplo, a pressão e a temperatura (uma reação pode ter um Kc muito elevado, mas, à temperatura considerada, ser muito lenta).
⇒ O rendimento de uma reação depende das condições em que reação ocorre, como, por exemplo, existência de reações paralelas, perdas do produto nos processos de separação, etc.
ou
⇒ A constante de equilíbrio está relacionada com a extensão das reações químicas.
⇒ Um valor elevado da constante de equilíbrio significa que a reação, à temperatura considerada, é muito extensa, ou seja, a formação dos produtos da reação é favorecida, uma vez que no equilíbrio o produto dos valores numéricos das concentrações dos produtos da reação elevados aos respetivos coeficientes estequiométricos é muito maior do que o produto dos valores numéricos das concentrações dos reagentes elevados aos respetivos coeficientes estequiométricos.
- Opção (A) ……………. 10 pontos
GRUPO V
O dióxido de carbono reage com a água, dando origem ao ácido carbónico, H2CO3 (aq).
O ácido carbónico é um ácido diprótico que se ioniza em água em duas etapas sucessivas, traduzidas por
H2CO3 (aq) + H2O (l) ⇋ HCO3– (aq) + H3O+ (aq) (1)
HCO3– (aq) + H2O (l) ⇋ CO32- (aq) + H3O+ (aq) (2)
- 11ºano – Química – Domínio 2 – subdomínio 1 (Reações ácido-base)
1. Apresente a expressão que traduz a constante de acidez, Ka , do ácido carbónico, definida para a reação (1).
- 11ºano – Química – Domínio 2 – subdomínio 1 (Reações ácido-base)
2. A espécie HCO3– (aq) é a base conjugada de _____ e o ácido conjugado de ______.
(A) H2CO3 (aq) … H2O (l)
(B) H2O (l) … H2CO3 (aq)
(C) H2CO3 (aq) … CO32- (aq)
(D) CO32- (aq) … H2CO3 (aq)
- Opção (C)
⇒ Uma base conjugada de um ácido de Brönsted-Lowry é a espécie química que resulta da perda de um protão, ião H+, pelo ácido.
- Assim, a espécie HCO3– é a base conjugado do ácido H2CO3.
⇒ A espécie CO32- é a base conjugada da espécie HCO3–.
- Opção (C) ……………. 10 pontos
- 11ºano – Química – Domínio 2 – subdomínio 1 (Reações ácido-base)
3. A preservação de estruturas vitais de alguns organismos marinhos, como as conchas, cujo principal componente é o carbonato de cálcio, CaCO3 , depende do equilíbrio que se estabelece entre este sal sólido e os iões resultantes da sua dissolução em água.
Esta reação pode ser traduzida porCaCO3 (s) ⇋ Ca2+ (aq) + CO32- (aq)
Preveja, fundamentando, se a diminuição do pH das águas dos oceanos contribui para a preservação das conchas ou, pelo contrário, para a sua dissolução.
Escreva um texto estruturado, utilizando linguagem científica adequada.
⇒ A diminuição do pH das águas dos oceanos resulta de um aumento da concentração de H3O+ (aq).
⇒ De acordo com o Princípio de Le Châtelier, o aumento de H3O+ (aq) favorece o sentido inverso da reação (2), com consequente diminuição da concentração de iões carbonato, CO23- (aq), nas águas dos oceanos.
⇒ Por sua vez, esta diminuição de iões carbonato favorece, de acordo com o Princípio de Le Châtelier, a dissolução do carbonato de cálcio, CaCO3 (s).
⇒ Prevê-se, assim, que a diminuição do pH das águas dos oceanos contribui para a dissolução das conchas de organismos marinhos.
- Fundamentação:
⇒ aumento da concentração do ião H3O+ (aq) nas águas dos oceanos e favorecimento da reação (2) no sentido inverso;
⇒ diminuição da concentração do ião CO32− (aq) e favorecimento da dissolução do CaCO3.
- Previsão: a diminuição do pH das águas dos oceanos contribui para a dissolução das conchas.

FIM






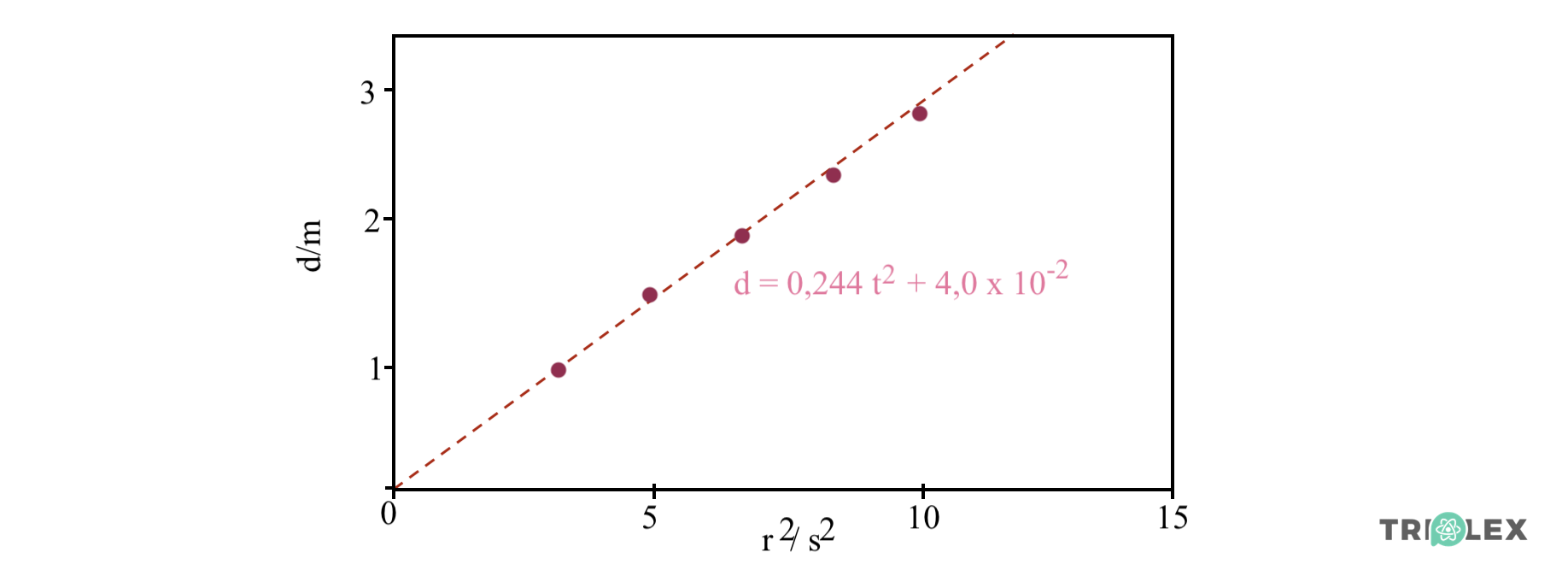











um dos meus favoritos até agora 8/10
Muito bem, continua.
*O mais fácil até agora 10/10
Parabéns